はじめに

回帰に関する記事です。本記事では多項ロジスティック回帰について扱います。

本記事の目次は以下の通りです。

• はじめに
• 多項ロジスティック回帰の説明
• データの入手と内容の確認
• 分析手法の検討
  • 順序ロジスティック回帰
  • 従属変数を2値に統合し、通常のロジスティック回帰を行う
• 分析の実行
• 結果の描画
• まとめ

多項ロジスティック回帰の説明

多項ロジスティック回帰(multinomial logisticregression)は3つ以上の値をとる名義尺度$Y$を従属変数とし、説明変数$X$から$Y$のそれぞれの値をとる確率を説明しようとする回帰手法です。

今、$Y=(y_1,\dots ,y_n,\dots ,y_N{)}^T$、$X=(x_1,\dots ,x_n,\dots ,x_N{)}^T$とし、さらに $x_n=(x_{1n},\dots ,x_{dn},\dots ,x_{Dn})$とします。ここでNはサンプルサイズ、Dは説明変数の次元です。

$Y$のとる値が2値のみの場合はロジスティック回帰と呼ばれます。これはリンク関数としてロジスティック関数が用いられますが、一方で$Y$がとることのできる値の数が$K\ge 3$のとき多項ロジスティック回帰が用いられ、この場合ソフトマックス関数が用いられます。

多項ロジスティック回帰のモデル式は以下の通りです。

$${\mu }_n=\overrightarrow{a}+\overrightarrow{b_1}{x}_{n1}+\cdots +\overrightarrow{b_d}{x}_{nd}+\cdots +\overrightarrow{b_D}{x}_{nD}$$ $${\theta }_n=\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}({\mu }_{\mathrm{n}})$$ $$y_n\sim \mathrm{C}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{g}\mathrm{o}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{a}\mathrm{l}({\theta }_{\mathrm{n}})$$ $$(n=1,\dots ,N)$$

ここで $$\mu =({\mu }_1,\dots ,{\mu }_n,\dots ,{\mu }_N)$$ $$\theta =({\theta }_1,\dots ,{\theta }_n,\dots ,{\theta }_N)$$

${\mu }_n,{\theta }_n,\overrightarrow{a},\overrightarrow{b_1},\dots ,\overrightarrow{b_D}$は長さKのベクトルです。
$\mu$は一般化線形モデルの枠組みでは線形予測子と呼ばれる部分で、ここではK個の線形予測子が準備される形です。

ソフトマックス関数は下記式で与えられます。

$$\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}(\mathrm{m}{\mathrm{u}}_{\mathrm{n}})=(\frac{\exp (\mathrm{m}{\mathrm{u}}_{1\mathrm{n}})}{\sum _{\mathrm{k}=1}^{\mathrm{K}}\exp (\mathrm{m}{\mathrm{u}}_{\mathrm{k}\mathrm{n}})}\cdots \frac{\exp (\mathrm{m}{\mathrm{u}}_{\mathrm{K}\mathrm{n}})}{\sum _{\mathrm{k}=1}^{\mathrm{K}}\exp (\mathrm{m}{\mathrm{u}}_{\mathrm{k}\mathrm{n}})})$$

ソフトマックス関数は各要素が$(0,1)$の範囲をとり合計1になる長さ$K$のベクトルであり、カテゴリカル分布に与える確率ベクトルとして用います。最終的には$Y$が${\theta }_n$を確率ベクトルとしてもつカテゴリカル分布に従うと仮定することになります。

なお、上記のモデルそのままでは$\mu$の$K$個の要素が識別不可能であるため$Y$がとりうる$K$個の値それぞれにに対応させることができません。そのため、$K$個の要素のうち基準となる要素を一つ決め、 $\mu$の$K$個の要素を識別できるように

$$a_k=b_{1k}=\dots =b_{Dk}=0$$ $$\therefore {\mu }_{nk}=0(n=1,\dots ,N)$$

と基準とした要素を0に固定してやる必要があります($k$は0から$K$のどの値でも構いません)。よってパラメータ数は$(D+1)(K-1)$となります。

本記事はこちらのページを参考に作成しました。内容的にはほとんど同じで、つまりただ真似してやってみただけです…。

データの入手と内容の確認

SPSS、Stata等に蓄積されているデータをダウンロードするためのパッケージforeignを使ってデータを入手し、簡単に内容を確認しておきます。

library(foreign)
ml <- read.dta("https://stats.idre.ucla.edu/stat/data/hsbdemo.dta")
head(ml)

##    id female    ses schtyp     prog read write math science socst       honors
## 1  45 female    low public vocation   34    35   41      29    26 not enrolled
## 2 108   male middle public  general   34    33   41      36    36 not enrolled
## 3  15   male   high public vocation   39    39   44      26    42 not enrolled
## 4  67   male    low public vocation   37    37   42      33    32 not enrolled
## 5 153   male middle public vocation   39    31   40      39    51 not enrolled
## 6  51 female   high public  general   42    36   42      31    39 not enrolled
##   awards cid
## 1      0   1
## 2      0   1
## 3      0   1
## 4      0   1
## 5      0   1
## 6      0   1

with(ml, table(ses, prog))

##         prog
## ses      general academic vocation
##   low         16       19       12
##   middle      20       44       31
##   high         9       42        7

with(ml, do.call(rbind, tapply(write, prog, function(x) c(M=mean(x), SD=sd(x)))))

##                 M       SD
## general  51.33333 9.397775
## academic 56.25714 7.943343
## vocation 46.76000 9.318754

このデータは200人の生徒について、性別等の属性や受賞数、読み書きの力を得点化したもの等がまとめられています。

今回は、general、academic、vocationの3つの授業プログラムの中から生徒が選択したプログラムの種類(prog)を従属変数とし、ses(経済的位置の3段階分類)、write(書く力を得点化したもの)を説明変数と設定します。

sesとprogのクロス集計表を見ると、いずれもsesにおいてもacademicが人気ですがses=highの子には特にacademicが人気なようです。

write毎のprogの平均、標準偏差を確認すると、やはりacademicを選んだ生徒は書く力が若干高いようです。

分析手法の検討

分析の目的は生徒の属性や能力が選択するプログラムにどのように影響してくるかを把握することですが、今回適用する多項ロジスティック回帰の他にいくつか別の手法も考えられます。

順序ロジスティック回帰

従属変数を順序データと解釈するモデルです。従属変数を$(Y=1,2,\dots ,k)$といった順序型の変数とみなしたとき、このモデルから得られる結果は 　　 $$P_{(y_n=2,\dots ,K)}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}({\mathrm{q}}_{1\mathrm{n}}), {\mathrm{q}}_{\mathrm{n}}=\mathrm{i}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\mathrm{a}}_1+{\mathrm{b}}_1{\mathrm{x}}_{\mathrm{n}1}+{\mathrm{b}}_2{\mathrm{x}}_{\mathrm{n}2}+\dots +{\mathrm{b}}_{\mathrm{D}}{\mathrm{x}}_{\mathrm{n}\mathrm{D}})$$ $$P_{(y_n=3,\dots ,K)}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}({\mathrm{q}}_{2\mathrm{n}}), {\mathrm{q}}_{\mathrm{n}}=\mathrm{i}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\mathrm{a}}_2+{\mathrm{b}}_1{\mathrm{x}}_{\mathrm{n}1}+{\mathrm{b}}_2{\mathrm{x}}_{\mathrm{n}2}+\dots +{\mathrm{b}}_{\mathrm{D}}{\mathrm{x}}_{\mathrm{n}\mathrm{D}})$$ $$\dots$$ $$P_{(y_n=K)}\sim \mathrm{B}\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{i}\mathrm{a}\mathrm{l}({\mathrm{q}}_{(\mathrm{K}-1)\mathrm{n}}), {\mathrm{q}}_{\mathrm{n}}=\mathrm{i}\mathrm{n}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{i}\mathrm{t}({\mathrm{a}}_{\mathrm{K}-1}+{\mathrm{b}}_1{\mathrm{x}}_{\mathrm{n}1}+{\mathrm{b}}_2{\mathrm{x}}_{\mathrm{n}2}+\dots +{\mathrm{b}}_{\mathrm{D}}{\mathrm{x}}_{\mathrm{n}\mathrm{D}})$$

のk-1個の確率に関する回帰式となります。

上記モデルでは、$Y$を一つの順序型変数とみなすという設定に合わせ、解釈上の都合から(?)切片項以外の係数を全回帰式で同一としています。

今回のデータでは説明変数が通常の授業(general)、アカデミックな授業(academic)、職を持つための授業(vocation、高専のようなイメージ？)といった内容のものであるため、順序型データとはみなさないこととします。

従属変数を2値に統合し、通常のロジスティック回帰を行う

多項ロジスティック回帰は得られる結果の解釈が難しいという欠点があるため、より解釈がし易いようにデータを簡略化し、通常のロジスティック回帰に持ち込む方法です。今回の例ではacademicを選択する確率に着目し、generalとvocationを一つにまとめる、といったことが考えられます。

ここでは3つの授業を選択する確率同士の間に説明変数を介してどのような関係があるのかを把握することを選択し、多項ロジスティック回帰を選びます。

分析の実行

nnetパッケージのmultinom()を用いて分析していきます。nnetは最尤法を用いて単層のニュートラルネットワークを実行するためのパッケージで、multinom()は単層のニュートラルネットワークを介して多項対数線形モデルを行う関数です。$x_n$に着目したとき、単層のニュートラルネットワークのK個の中間層を

$$\mathrm{中}\mathrm{間}\mathrm{層}k=\exp (\overrightarrow{a_k}+\overrightarrow{b_{1k}}{x}_{n1}+\cdots +\overrightarrow{b_{dk}}{x}_{nd}+\cdots +\overrightarrow{b_{Dk}}{x}_{nD})k=1,\dots ,K$$ 、出力層を

$$(\frac{exp(\mathrm{中}\mathrm{間}\mathrm{層}1)}{\sum _{k=1}^K\mathrm{中}\mathrm{間}\mathrm{層}k}\cdots \frac{exp(\mathrm{中}\mathrm{間}\mathrm{層}K)}{\sum _{k=1}^K\mathrm{中}\mathrm{間}\mathrm{層}k})$$

としてやれば多項ロジスティック回帰モデルと等価になる(はず…ニュートラルネットはよく知りません)ですので、中身はそのような形になっているものと思われます。

$\mu$のK個の要素を識別可能とするため、下記の実行では${\mu }_{academic}=0$としています。
またmultinom()はp値を出力してくれないので、両側Z検定を行いp値を算出します。

library(nnet)
#academicを基準に設定
ml$prog2 <- relevel(ml$prog, ref = "academic")
test <- multinom(formula = prog2 ~ ses + write, data=ml)

## # weights:  15 (8 variable)
## initial  value 219.722458
## iter  10 value 179.982880
## final  value 179.981726
## converged

summary(test)

## Call:
## multinom(formula = prog2 ~ ses + write, data = ml)
##
## Coefficients:
##          (Intercept)  sesmiddle    seshigh      write
## general     2.852198 -0.5332810 -1.1628226 -0.0579287
## vocation    5.218260  0.2913859 -0.9826649 -0.1136037
##
## Std. Errors:
##          (Intercept) sesmiddle   seshigh      write
## general     1.166441 0.4437323 0.5142196 0.02141097
## vocation    1.163552 0.4763739 0.5955665 0.02221996
##
## Residual Deviance: 359.9635
## AIC: 375.9635

#両側Z検定の実行
z <- summary(test)$coefficients/summary(test)$standard.errors
p <- (1 - pnorm(abs(z),0,1))
p

##           (Intercept) sesmiddle    seshigh        write
## general  7.238305e-03 0.1147190 0.01186928 3.409451e-03
## vocation 3.649650e-06 0.2703765 0.04947488 1.588023e-07

結果は下記式に帰着します(${}^{\ast \ast \ast }$：0.1%有意、${}^{\ast \ast }$：1%有意、${}^{\ast }$：5%有意)。

$$\frac{P(prog=general)}{P(prog=academic)}=\exp ({2.85}^{\ast \ast \ast }-0.53(ses=middle)-{1.16}^{\ast }(ses=high)-{0.06}^{\ast \ast \ast }write)$$

$$\frac{P(prog=vocation)}{P(prog=academic)}=\exp ({5.22}^{\ast \ast \ast }-0.29(ses=middle)-{0.98}^{\ast }(ses=high)-{0.11}^{\ast \ast \ast }write)$$

上記の結果は、generalを選択する確率とacademicを選択する確率のオッズ比

$$\frac{P(prog=general)}{P(prog=academic)}$$

に着目した場合、下記式のようにwriteの値が1増えるとオッズ比は0.94倍になる、というよう解釈できます。

ロジスティック回帰のモデルは、このように、基準に設定した値を分母としたオッズ比からの解釈がしやすい点が特徴です。

そのほかの係数について確認しておくと、

• $\frac{P(prog=vocation)}{P(prog=academic)}$はwriteの値が1増加すると$\exp (-0.11)\fallingdotseq 0.89$倍になる(有意)。

• $\frac{P(prog=general)}{P(prog=academic)}$は$ses=high$のとき、$ses=low$の時の$\exp (-1.16)\fallingdotseq 0.31$倍の値をとる(有意)。

• $\frac{P(prog=vocation)}{P(prog=academic)}$は$ses=high$のとき、$ses=low$の時の$\exp (-0.98)\fallingdotseq 0.38$倍の値をとる(有意)。

• $\frac{P(prog=general)}{P(prog=academic)}$は$ses=middle$のとき、$ses=low$の時の$\exp (-0.53)\fallingdotseq 0.59$倍の値をとる。ただしこの値は1である可能性を捨てきれない

• $\frac{P(prog=vocation)}{P(prog=academic)}$は$ses=middle$のとき、$ses=low$の時の$\exp (-0.29)\fallingdotseq 0.74$倍の値をとる。ただしこの値は1である可能性を捨てきれない

といった結果が得られています。

二番目の項目($\frac{P(prog=general)}{P(prog=academic)}$と$ses=high,ses=low$の関係)については下記式から確認できます。

$$\frac{\frac{P(prog=general(ses=high))}{P(prog=academic(ses=high))}}{\frac{P(prog=general(ses=low))}{P(prog=academic(ses=low))}}=\frac{\exp (2.85-0.53\times 0-1.16\times 1-0.06(write)}{\exp (2.85-0.53\times 0-1.16\times 0-0.06(write))}$$ $$=\exp (-1.16)\fallingdotseq 0.31$$

結果の描画

結果の描画を行います。ses,writeの値が1組与えられた時の予測値はpredict()関数で算出できます(信頼区間を求めようとしたらnnet::predict()はpredict=“confidence"が使えませんでした…残念)。
以下では予測値の算出を行っていますが、今回のモデルは解釈しやすいように設計されたモデルです。予測用のモデルにが欲しいなら更なる改良モデルが存在します。

library(reshape2)
library(ggplot2)
library(RColorBrewer)
#予測値を計算する点を準備
dwite <- data.frame(ses = rep(c("low","middle","high"),each = 41), write = rep(c(30:70),3))
#predict()関数で予測値を計算し、予測を行う点dwiteと結合
pp.wite <- cbind(dwite, predict(test, newdata=dwite, type="probs", se = T))
#縦長データに変換し、ggplot()で描画
lpp <- reshape2::melt(pp.wite, id.vars = c("ses","write"),value.name = "probability")
cols <= brewer.pal(3,"Dark2")
p0 <- ggplot(data=lpp,aes(x=write, y=probability,colour=ses)) + geom_line() + facet_grid(variable ~.) + theme_bw(base_size=11) +
  theme(legend.position = "bottom") + scale_color_manual(values=cols) + labs(title="With multinom")
p0

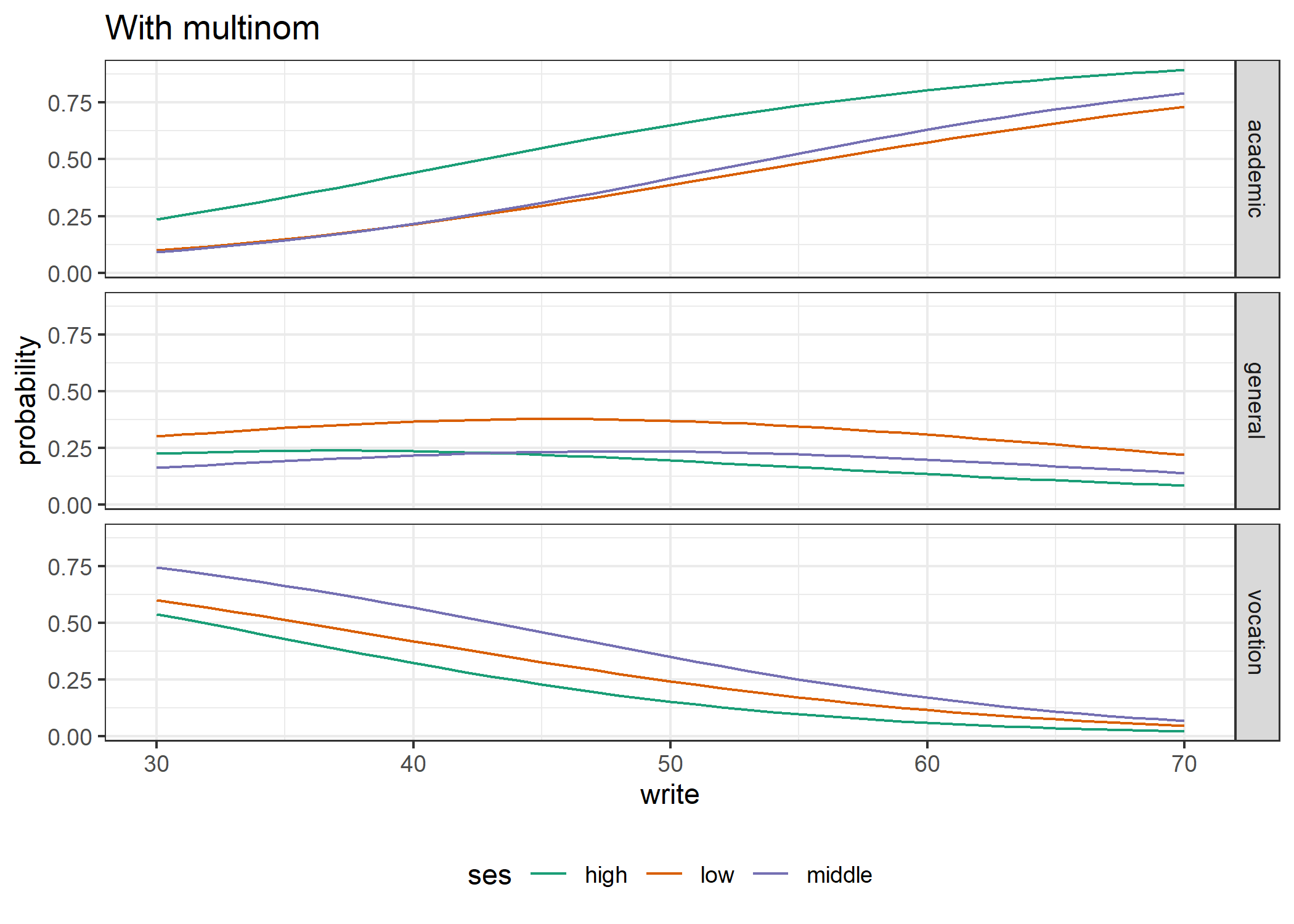
上図では3つの授業が選ばれる確率を別々に描画しています。同じ色の線がとる確率値の割をとると1になります。 図の全体的な傾向と前節で確認した内容に不一致は見られないようです。

まとめ

本記事では多項ロジスティック回帰モデルについて説明しました。
多項ロジスティック回帰は3つ以上の値をとる名義尺度$Y$を従属変数とし、説明変数$X$から$Y$のそれぞれの値をとる確率を説明しようとする回帰手法です。

また多項ロジスティック回帰自体は予測用のモデルではなく、あくまで解釈の為のモデルであることがポイントです。
本モデルを応用した予測用のモデルは今後の記事で紹介したいと思います。