はじめに
今までに幾度かテーマにしていますが、回帰とよばれる問題があります。
例えば、車の速度とブレーキをかけてから車が止まるまでの距離について、データから両者の関係を把握したい、というような場合。最も単純な関係式でこの目的を果たそうとする場合、一般には以下に示す単回帰が用いられるでしょう。
$$ \mu_n = ax_n + b $$ $$ y_n \sim \rm{Normal}(\mu_n, \sigma) $$ $$ n=1, \ldots, N $$
$Y$は目的変数(説明変数によって説明される変数)、$X$は説明変数(目的変数を説明する変数)、それぞれ$Y=(y_1, \ldots, y_n, \ldots, y_N)$、$X=(x_1, \ldots, x_n, \ldots, x_N)$です。
こんな需要もあるかもしれません。 上のモデルより少し難しいモデルですが、$X$、$Y$ともに非負の実数であることから、$Y$がガンマ分布に従うとし、リンク関数を$log$とした場合。 $$ \mu_n = \rm{exp}(ax_n + b) $$ $$ y_n \sim \rm{Gamma}(\mu_n, \alpha, \beta) $$
上記の内容について理解が追い付かない場合は、こちらのサイトなどを覗いてみてください。分かりやすくまとめられています。
分析の目的が変数間の関係把握であるならば、上述のモデルで事足りる場合も多いと思います。しかし「将来得られる可能性のある任意の値$X_{new}$に対応する$Y_{new}$の値を予測したい」というような場合、話は変わってきます。
これまでに得られたデータ$X$、$Y$の組から将来得られるデータ$X_{new}$に対応する$Y_{new}$の値を予測するとなると、より観測データにフィットできる柔軟なモデルを構築することが理想です(ただし過学習には要注意)。
今回は、上記のような期待に応えるモデルとしてガウス過程を取り上げ、 データに対し柔軟な回帰曲線を得られるようにすることを最終目標とします。
参考図書はこちらです。 こちらのブログも大いに参考にさせていただきました。RもいいですがJuliaも面白そうです。影響を受けてJuliaの参考書を買ってしまいました。
本記事の構成は以下の通りです。
ガウス過程の定義
ガウス過程の導出
ガウス過程について特にわかりやすいと思った参考図書の記載を抜粋してガウス過程について説明します。
この節の理解には多変量正規分布($\rm{MultiNormal}()$)の理解が必要です。多変量正規分布については参考図書などを見て適宜補完してください。
以下の線形回帰モデルを考えます。
特徴ベクトルの要素数を$H$とします。
特徴ベクトルとは機械学習分野の用語で、変換処理によって抽出されるデータの特徴を要素に持つベクトルです。
$\phi(x)$は説明変数群$X$(機械学習分野では入力と呼びます)の要素$x$に関する特徴ベクトルです。
$$ \phi(x) = (\phi_1(x), \phi_2(x), \phi_3(x), \ldots, \phi_H(x)) $$
$w$は各特徴の重みです。
$$ w = (w_1, w_2,w_3, \ldots, w_H)^T $$
$\hat{y}$を目的変数$Y$の要素$y$についての予測値とすると、
$$ \hat{y} = \phi(x)w \tag{1} $$
とおけます。
さらに式(1)を$(\hat{y}_1,x_1), \ldots, (\hat{y}_N,x_N)$についてまとめると、
$$
\left(
\begin{array}{ccc}
\hat{y}_1 \\
\hat{y}_2 \\
\vdots \\
\hat{y}_N
\end{array}
\right) =
\left(
\begin{array}{ccc}
\phi_1(x_1) & \phi_2(x_1) & \cdots & \phi_H(x_1) \\
\phi_1(x_2) & \phi_2(x_2) & \cdots & \phi_H(x_2) \\
\cdots & \cdots & \ddots & \cdots \\
\phi_1(x_N) & \phi_2(x_N) & \cdots & \phi_H(x_N)
\end{array}
\right)
\left(
\begin{array}{ccc}
w_1 \\
w_2 \\
\vdots \\
w_H
\end{array}
\right) \tag{2}
$$
とおけます。 ここで$\phi_{nh} = \phi_{h}(x_n)$を要素に持つ計画行列(統計モデルの基底関数についての行列)$\Phi$を使うと、式(2)は
$$ \hat{Y} = \Phi w \tag{3} $$
とまとめられます。
式(3)を使えば、基底関数を自由に設定したり、基底関数の次元を増やすことでほとんど任意の形の関数が表現できそうです。しかし、$x$が高次元であるほど基底関数の数を多く設定する必要があり、そうなるとパラメータ$w$もどんどん増えていってしまい、最終的にはパラメータ$w$の推定が不可能なほどになってしまいそうです。
そこで、パラメータwの周辺化消去(期待値をとって積分消去)を考えます。
$w$が平均0、分散$\lambda^2I$の互いに独立な正規分布に従うと仮定し、重み$w$が特定の基底関数に偏り、過学習に陥りにくいように設定します。
$$ w \sim \rm{MultiNormal}(0, \lambda^2I) \tag{4} $$
これによって$w$の期待値を仮定し、周辺化消去を行うのですが、その過程は省略し、結果のみを以下に書きます。
$$ Y \sim \rm{MultiNormal}(0, \lambda^2\Phi\Phi^T) \tag{5} $$
式(5)がガウス過程を定義する式です。これは式(3)と基本的に同じ機能をもつため、式(3)と同様、ほとんどどんな形でも表現できそうです。ただし、線形回帰モデル式(3)にあったパラメータ$w$が積分消去されているため、$x$の次元がいくら高くなっても推定するパラメータは増えず、$y$の分布はデータ数$N$に依存する共分散行列$\lambda^2\Phi\Phi^T$のみによって決定します。さらに式(3)からの変形で式(4)をかませているため、過学習に陥る可能性が抑えられています。
ガウス過程の直感的な性質
ガウス過程の性質を決定する共分散行列について見ていきます。
$$ K = \lambda^2\Phi\Phi^T $$
とおくと、この$(n, n^{'})$要素は
$$ k_{nn^{'}} = \lambda^2\phi(x_n)^T\phi(x_{n^{'}}) $$
なので、これは$x_{n}$と$x_{n^{'}}$の特徴ベクトル$\phi(x_{n})$と$\phi(x_{n^{'}})$の内積の$\lambda^2$倍です。多変量正規分布において2変数の共分散が大きいとき、両者の相関が高いということなので、2変数の平均値が同値かつ共分散が大きいとき、両者は似た値をとりやすくなります。
つまり、$x_{n}$と$x_{n^{'}}$が設定した特徴ベクトル空間において似ている場合、対応する$y_{n}$と$y_{n^{'}}$も似た値が出力されやすくなります。このように、説明変数$x$が似ていれば目的変数の予測値$y$も似た値となる、というのがガウス過程の性質になります。
カーネル関数
$$ k_{nn^{'}} = \phi(x_n)^T\phi(x_{n^{'}}) \tag{6} $$
これを特徴ベクトルから計算しようとすると、複雑な計算が要求されます。そうではなく、式(6)を計算するための関数として、カーネル関数を用います。また、カーネル関数を用いて内積を計算することをカーネルトリックと呼びます。
カーネル関数は、何らかの無限次元の特徴ベクトル空間における2点の内積を表現できる、という特徴をもつ関数で、それぞれに異なる無限次元特徴ベクトルを定義する様々なカーネル関数があります。
例えば、カーネル関数の1種、ガウスカーネル
$$ k(x,x_{'}) = \rm{exp}(-a(x-x^{'})^2) $$
の場合、
$$ \rm{exp}(-a(x-x^{'}))^2 = \phi(x)^{T}\phi(x^{'}) $$
となる特徴ベクトルは、第$r$成分が
$$ \phi_r(x) = \left(\cfrac{4a}{\pi}\right)^{\cfrac{1}{4}}\rm{exp}(-2a(x-r)^2) $$
となります($r$は実数で、$r=-\infty, \ldots, \infty$)。
これは、 $$ \int_{-\infty}^{\infty} \phi_r(x)\phi_r(x^{'}) dr = exp(-a(x-x^{'}))^2 $$
を証明することで確認できます。証明はこちらのサイトで見れます。
なお、通常のパラメータとは設定目的の異なる、モデルの複雑さを決定するパラメータはハイーパーパラメータ(超母数)などと呼ばれます。以降、カーネル関数のパラメータもハイパーパラメータと呼ぶことにします。
ガウス過程のシミュレーション
ガウス過程の概要を確認したので、ガウス過程に従う確率変数がどのような挙動をするのか、いくつかのカーネル関数を例に見てみます。
シミュレーションの前に、カーネル行列($K$のこと)を作成する関数と、シミュレーションのための関数を定義しておきます。
# カーネル行列を作成する関数を定義
# 引数 kernel:この後に定義するカーネル関数を指定 x:トレーニングデータ
# 引数 par:kernelが要求するハイパーパラメータ delta:誤差の要素。ハイパーパラメータとは別で指定することにした
kernel_cov <- function(kernel, x,par, delta){
NL <- length(x)
Sigma <- matrix(NA, nrow=NL, ncol=NL)
for(i in 1:(NL-1)){
Sigma[i,i] <- kernel(x[i],x[i],par) + delta
for(j in (i+1):NL){
Sigma[i,j] <- kernel(x[i],x[j],par)
Sigma[j,i] <- Sigma[i,j]
}
}
Sigma[NL,NL] <- kernel(x[NL],x[NL],par) + delta
return(Sigma)
}
# シミュレーションのための自作関数を定義
GP_sim <- function(kernel, par){
p <- ggplot() + theme_bw(base_size = 11)
i <- 0
xs = seq(-4,4,0.05)
repeat{
i <- i + 1
if(i == 5) break
p <- p + geom_line(data=data.frame(x = xs,
y = MASS::mvrnorm(1, mu=rep(0,length(xs)),
kernel_cov(kernel=kernel,x=xs, par=par,delta=1e-8))),
aes(x=x,y=y), colour=as.factor(i))
}
plot(p)
}
ガウスカーネルのシミュレーション
前の節で紹介したガウスカーネルのシミュレーションです。改めてガウスカーネルを再定義します。
ガウスカーネルは、下のようにrateパラメータ$\theta$、shapeパラメータ$\rho$をもちます。ここでは$\theta$、$\rho$ともに1とした場合のシミュレーションをします。
$$ k(x,x_{'}) = \theta \rm{exp}\left(-\cfrac{(x-x^{'})^2}{\rho}\right) $$
## ガウスカーネルの定義 kernel_cov()で使用できるように、引数は(x1,x2,par)でないといけない
## カーネルのハイパーパラメータはすべてparで指定する
Gaussian_kernel <- function(x1, x2, par){
return(par[1]*exp(-(x1 - x2)^2/par[2]))
}
GP_sim(Gaussian_kernel, par=c(1,1))
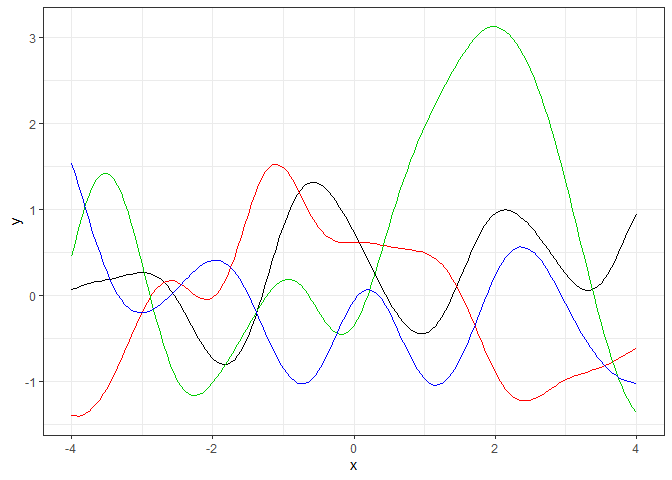
ガウスカーネルをカーネル関数に設定したガウス過程は、無限回微分可能な滑らかな曲線になるそうです。
線形カーネルのシミュレーション
線形カーネルは、ハイパーパラメータを持たないカーネル関数です。
$$ k(x,x_{'}) = x^T x^{'} $$
線形カーネルは、$\phi(x)=x$としているので、これを式(1)に代入すると、$x$の中に定数項$x_0=1$が含まれているとした場合、通常の重回帰と等価であることが分かります。
## 線形カーネルを定義。ハイパーパラメータは無し
linear_kernel <- function(x1,x2,par){
return(1 + t(x1)%*%x2)
}
GP_sim(linear_kernel, par=NULL)
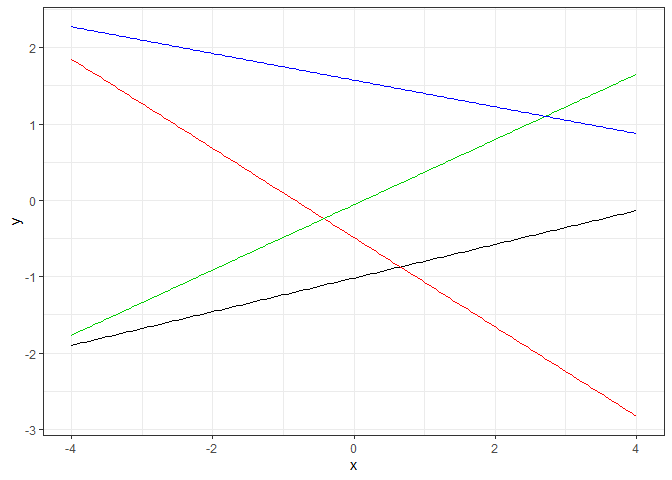
シミュレーションでも直線が引けることが確認できます。
Matern3カーネルのシミュレーション
Maternカーネルは、ガウスカーネルの無限回微分可能という前提がモデル化において強すぎるという主張から提案されたカーネルです。
$$ k_v(x,x^{'}) = \cfrac{2^{1-\upsilon}}{\Gamma(\upsilon)} \left( \cfrac{\sqrt{2\upsilon}r}{\upsilon} \right)^2 K_v \left( \cfrac{\sqrt{2\upsilon}r}{\upsilon} \right) ~~~ (r=|x-x^{'}|) $$
Maternカーネルを用いたガウス過程から生成される関数は、「$\upsilon$以下の最大の整数」回分微分可能で、$\upsilon$は$\cfrac{3}{2},\cfrac{5}{2} $などが使われ、それぞれMatern3、Matern5と呼ばれるようです。
Matern3カーネルは以下のようになります。
$$ k_{3/2}(x,x^{'}) = \left(1 + \cfrac{\sqrt{3}r}{\theta} \right) exp\left( -\cfrac{\sqrt{3}r}{\theta} \right) $$
このMatern3カーネルを$\theta=1$としてシミュレーションしてみます。
# Matern3カーネルを定義
Matern3_kernel <- function(x1,x2, par){
return((1 + sqrt(3)*abs(x1-x2)/par[1])*exp(-sqrt(3)*abs(x1-x2)/par[2]))
}
GP_sim(Matern3_kernel,par=c(1,1))
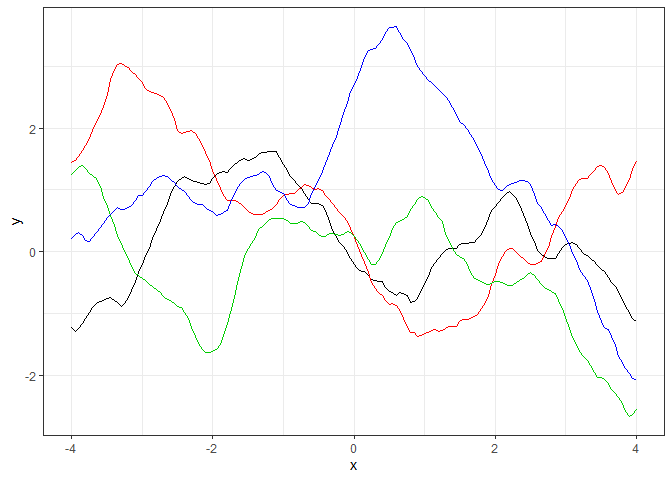
ガウスカーネルと比べていびつな曲線になっていることが分かります。
ガウスカーネルと線形カーネルの結合
カーネル関数は組み合わせて使うことも可能です。 ここではガウスカーネルと線形カーネルを組み合わせてみます。
$$ k(x,x_{'}) = \theta_1 \rm{exp}\left(-\cfrac{(x-x^{'})^2}{\rho}\right) + \theta_2x^T x^{'} $$
上の式において、$\theta_1=0.8, \theta_2=2, \rho=0.07$としたときのシミュレーションです。
# ガウスカーネル+線形カーネルの定義
Gaussian_plus_Linear_kernel <- function(x1,x2,par){
return(par[1] * exp(-(x1 - x2)^2/par[2]) + par[3] * (1 + t(x1)%*%x2))
}
GP_sim(Gaussian_plus_Linear_kernel,c(0.8,0.07,2))

ガウスカーネルと線形カーネルがうまく組み合わさっていることが分かります。
実際に回帰・パラメータ推定を実行
ひととおりシミュレーションしたので実践です。 まずは参考図書と同じ、陸上男子100mの世界記録のデータを準備します。$x$は世界記録更新日、$y$は世界記録のタイムです。
# データの準備
x <- as.Date(x=c("1964/10/15","1968/6/20","1968/10/13","1968/10/14","1983/7/3","1987/8/30","1988/8/17",
"1988/9/24","1991/7/14","1991/8/25","1994/7/6","1996/7/27","1999/6/16","2002/9/14",
"2005/6/14","2006/5/12","2006/6/11","2006/8/18","2007/9/9","2008/5/31","2008/8/16","2009/8/16"))
y <- c(10.06,10.03,10.02,9.95,9.93,9.93,9.93,9.92,9.9,9.86,9.85,9.84,9.79,9.78,9.77,9.77,9.77,9.77,9.74,9.72,9.69,9.58)
# 標準化
x <- (as.numeric(x)-mean(as.numeric(x)))/sd(as.numeric(x))
y <- (y-mean(y))/sd(y)
library(ggplot2)
p <- ggplot(data=data.frame(x=x,y=y), aes(x=x,y=y)) + theme_bw(base_size=11) + geom_point()
p

分析にあたって、まずはハイパーパラメータの最適な値を推定します。 推定方法にはハイパーパラメータを少しずつ変えてその事後分布を推定するMCMCも使えますが、ここでは計算量の少ない効率的な方法として勾配法を用います。 簡略化のため、ガウス過程のハイパーパラメータを$\theta=(\theta_1, \theta_2,\ldots)$とまとめておき、カーネル行列も$K_{\theta}$とします。 確率変数$Y$がガウス過程$GP(0,K_\theta)$に従うと仮定したとき、観測値に対する尤度は、
$$ p(Y|X,\theta) = \rm{MultiNormal}(Y|o,K_{\theta}) = \cfrac{1}{(2\pi)^{N/2}} \cfrac{1}{|K_{\theta}|^{1/2}} exp\left(\cfrac{1}{2}Y^TK_{\theta}^{-1}Y\right) $$
対数尤度は、
$$ \log(Y|X,\theta)~~ = ~~ -\cfrac{N}{2}\log(2\pi)-\cfrac{1}{2}\log|K_{\theta}|-\cfrac{1}{2}Y^TK_{\theta}^{-1}Y~~ \propto~~ -\log|K_{\theta}|-Y^TK_{\theta}^{-1}Y +(定数) \tag{7} $$
です。
式(7)を最大にする$\theta$を求め、ハイパーパラメータの最適な値とします。
式(7)を計算する自作関数を以下で定義します。
# ガウス過程モデルの対数尤度に比例する値を計算する関数を定義
GP_L <- function(x, y, par, kernel){
return(-log(det(kernel_cov(kernel=kernel,x=x,par=exp(par[-length(par)]),delta=exp(par[length(par)]))))
-t(y)%*%
solve(kernel_cov(kernel=kernel,x=x,par=exp(par[-length(par)]), delta=exp(par[length(par)])))%*%y)
}
式(7)を最大にする$\theta$は、Rの汎用最適化関数のoptim()を使います。参考図書では式(7)を$\theta$の各ハイパーパラメータで偏微分した式が紹介されています。optim()では引数grで一階偏微分関数を指定でき、簡単に定義できるなら明示的に指定した方が良いのですが、指定しなくても勝手に微分してくれるので今回は横着します。
参考図書には、以下のガウス過程の予測分布の公式が記載されていますので、この公式に倣って予測分布を計算する自作関数を定義します。
$$ p(Y^{\star}|X^{\star},\mathcal{D}) = \rm{MultiNormal}(k_{\star}^T K^{-1}Y,k_{\star\star}-k_{\star}^{T}K^{-1}k_{\star}) $$
ここで$\mathcal{D}$は観測値$Y$、$X$の$N$個のペア、$Y^{\star}=(y_1^{\star},\ldots,y_M^{\star})$、$X^{\star}=(x_1^{\star}, \ldots, x_M^{\star})$はそれぞれ予測値と特徴ベクトル空間における予測したい点の$M$個のペアです。$k_{\star}$、$k_{\star\star}$はそれぞれ $$ k_{\star}(n,m) = k(x_n,x_m^{\star})~~~(n=1,\ldots,N,m=1,\ldots,M) $$ $$ k_{\star\star}(m_1,m_2) = k(x_{m1}^{\star},x_{m2}^{\star})~~~(m_1=1,\ldots,M, m_2=1,\ldots,M) $$
を要素に持つカーネル行列です。
# 予測値の算出のための関数定義
# 返り値は各予測点の平均と共分散行列
my_predict <- function(x_test, x_train, y_train, kernel, par){
kernel_cov_star <- function(x1,x2,par,kernel){
NL <- length(x1)
ML <- length(x2)
Sigma <- matrix(NA, nrow=NL, ncol=ML)
for(i in 1:NL){
for(j in 1:ML){
Sigma[i,j] <- kernel(x1=x1[i], x2=x2[j],par=par[-length(par)])
}
}
return(Sigma)
}
K <- kernel_cov(kernel=kernel,x=x_train, par=par[-length(par)], delta=par[length(par)])
k_star <- kernel_cov_star(kernel=kernel, x1=x_train, x2=x_test,par=par)
k_2star <- kernel_cov(kernel=kernel, x=x_test, par=par[-length(par)], delta=par[length(par)])
mu <- t(k_star) %*% solve(K) %*% y_train
sigma <- k_2star - t(k_star) %*% solve(K) %*% k_star
return(list(mu, sigma))
}
ガウスカーネルを使った回帰
上で定義した関数を使い、カーネル関数にガウスカーネルを設定して回帰を実行してみます。
#自作関数GP_L()を使って対数尤度を計算 対数尤度を最大化するハイパーパラメータを推定
res_optim1 <- optim(par=c(0,0,0),fn=GP_L,kernel=Gaussian_kernel, x=x,y=y,control = list(fnscale=-1), method="BFGS")
par <- exp(res_optim1$par)
# 推定したパラメータの値を確認
par
## [1] 1.55308949 0.22898734 0.04299662
#自作関数my_predict()を使って予測分布の平均・ 共分散行列を求める
pre <- my_predict(x_test = seq(-2.0,2.0,0.01),x_train=x, y_train=y, kernel=Gaussian_kernel,par=par)
# 結果の描画
library(ggplot2)
p <- ggplot() + theme_bw(base_size=11) +
geom_line(data=data.frame(x=seq(-2.0,2.0,0.01),y=pre[[1]]),aes(x=x,y=y))
p <- p + geom_point(data=data.frame(x=x,y=y),aes(x=x,y=y))
p <- p + geom_ribbon(data=data.frame(x=seq(-2.0,2.0,0.01),ymin=pre[[1]]-2*sqrt(diag(pre[[2]])), ymax=pre[[1]]+2*sqrt(diag(pre[[2]]))),
aes(x=x,ymax=ymax,ymin=ymin),fill="blue",alpha=0.5)
p
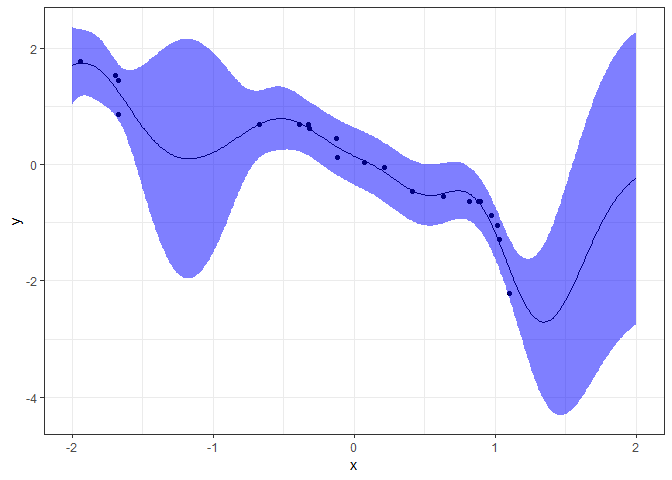
最適化したカーネル関数は以下になります。$\delta(x,x^{'})$はクロネッカーのデルタと呼ばれ、$x=x^{'}$のとき、つまりカーネル行列の対角成分にときのみ1を、それ以外は0を返す関数です。
$$ k(x,x_{'}) = 1.553exp\left(-\cfrac{(x-x^{'})^2}{0.229}\right) + 0.043\delta(x,x^{'}) $$
青い領域はガウス事後分布の$\pm2\sigma$の誤差範囲を示します。
これまた不思議な予測曲線が得られました。結果を観察すると、観測値の乏しい範囲では誤差範囲が広く推定されており、期待値も平均($=0$)に近づくようになっています。
ハリボーはこう考えました。
データの少ない部分は曖昧に推定するというのは、現実的な判断じゃあないか>🦔
しかしかめきちはこう言っています。
将来世界記録のタイムが伸びるという推定はあまりにもおかしいかめ>🐢
ガウスカーネル+線形カーネルで回帰
かめきちの意見を踏まえ、カーネル関数でガウスカーネルと線形カーネルを組み合わせてみます。
# ガウスカーネル+線形カーネを使って回帰
# 自作関数GP_L()を使って尤度を計算 尤度を最大化するハイパーパラメータを推定
res_optim2 <- optim(par=c(0,0,0,0),fn=GP_L,kernel=Gaussian_plus_Linear_kernel,
x=x,y=y,control = list(fnscale=-1), method="BFGS")
par <- exp(res_optim2$par)
# 推定したパラメータの値を確認
par
## [1] 0.11098682 0.02720031 0.46865763 0.04742707
# 自作関数my_predict()を使って予測分布の平均・ 共分散行列を求める
pre <- my_predict(x_test = seq(-2.0,2.0,0.01),x_train=x, y_train=y,
kernel = Gaussian_plus_Linear_kernel,par=par)
# 結果の描画
library(ggplot2)
p <- ggplot() + theme_bw(base_size=11) +
geom_line(data=data.frame(x=seq(-2.0,2.0,0.01),y=pre[[1]]),aes(x=x,y=y))
p <- p + geom_point(data=data.frame(x=x,y=y),aes(x=x,y=y))
p <- p + geom_ribbon(data=data.frame(x=seq(-2.0,2.0,0.01),ymin=pre[[1]]-2*sqrt(diag(pre[[2]])), ymax=pre[[1]]+2*sqrt(diag(pre[[2]]))),
aes(x=x,ymax=ymax,ymin=ymin),fill="blue",alpha=0.5)
p

It’s so brilliant>🐢
最適化したカーネル関数は以下になります。
$$ k(x,x_{'}) = 0.111exp\left(-\cfrac{(x-x^{'})^2}{0.027}\right) + 0.469x^T x^{'} + 0.047\delta(x,x^{'}) $$
タイムが短縮される全体的な傾向が線形カーネルでとらえるとともに、細かい変動をガウスカーネルで表現できています。
勾配法の初期値を変えるとどうなるでしょう。
res_optim3 <- optim(par=c(0,0.4,0,0),fn=GP_L,kernel=Gaussian_plus_Linear_kernel,
x=x,y=y,control = list(fnscale=-1), method="BFGS")
par = exp(res_optim3$par)
par
## [1] 0.22313442 2.81135418 0.50883359 0.09808983
~省略~

最適化したカーネル関数は以下になります。
$$ k(x,x_{'}) = 0.223exp\left(-\cfrac{(x-x^{'})^2}{2.811}\right) + 0.509x^T x^{'} + 0.098\delta(x,x^{'}) $$
ハイパーパラメータの値が変化し、結果も全く異なります。勾配法によるハイパーパラメータ推定では初期値によって結果が異なることも多く、局所最適解が多い場合はその傾向が強いです。
このような場合、MCMCで推定すると大域的局所解に近づいてくれます。
情報量基準の確認
モデルの良さを表す数値的指標として、各種の情報量基準が提案されています。 ここでは、以下で定義されるAICを計算してみます。 (AICは正しい使い方というのがあるようで私はAICを誤用しているかもしれません。誤りがあればご指摘を!)
$$ AIC = -2最大対数尤度+2自由パラメータの個数 $$
# optim()で対数尤度にマイナスをかけているので、ここでは対数尤度にマイナスをかけない
# optim()で最大化したGP_L()は、実際の対数尤度ではなく対数尤度に比例する値なので、ここで正確な対数尤度を計算する
my_AIC <- function(res_optim, x){
return(2*(res_optim$value/2 + length(x)/2 * log(2*pi))+2*length(res_optim$par))
}
cat(sprintf("AIC of \n res1 = %.3f\n res2 = %.3f\n res3 = %.3f",my_AIC(res_optim1,x), my_AIC(res_optim2,x), my_AIC(res_optim3,x)))
## AIC of
## res1 = 60.507
## res2 = 68.203
## res3 = 65.642
AICは、小さい値をとるモデルほど良いモデルと考えます。結果を見ると、一番初めのガウスカーネルを使ったモデルが最もAICが小さいです。また、ガウスカーネル・線形カーネルの2モデルの比較では、後のモデルの方がAICが小さいです。
これらの結果から、ガウスカーネルを使ったモデルが最も良いモデルであることが示唆されますが、AICはほかのモデルを完全否定するものではないので、最終的にどのモデルを選択するかは技術者判断と言えます。
私としては最後の結果を支持したいところです…。
まとめ
今回はガウス過程について説明しました。ガウス過程は理論が難しいですが、結果が合理的で、黒魔術かと疑ってしまうような技術です。
その応用範囲も広く、空間統計の分野では割と以前から活用されていたようです。また構造計算で利用される有限要素法においてもデータを完璧に補間するモデルとして広く利用されているそうです。
私はこれまで以下の活用方法を確認しています。
- 一般化線形モデルの線形予測子をガウス過程に置き換え、柔軟なモデルに豹変させる
- 空間統計において空間的自己相関を考慮したモデルを構築する
ちなみにガウス過程を一般化線形モデルに活用したりするような場合、事後分布は単純なガウス分布ではないため、MCMC等の近似推論法が必要となります。私の大好きなMCMCです。
また、大規模データに対しガウス過程を含むモデルを素直に計算すると、計算量が膨大となってしまいます。そのため、様々な近似手法が提案されているようです。参考図書の後半でその近似手法が述べられているので今後勉強したいと思っています。
ガウス過程の活用例も今後の記事で紹介できればと思っています。楽しみ。
