はじめに
いい夢の色は緑色だそうだ。私もうさぎさんにとっての牧草色の夢を見ることもありますが、現実は柵に引っかかってばかりです。
さて、回帰に関する記事です。
以前の記事では、対象が3つ以上のクラスに分類されるとき、それぞれのクラスに属する確率を予測するモデルである多項ロジスティック回帰について書きました。
次の記事では、同様のモデルを、マルコフ連鎖モンテカルロ法(MCMC)を実行するための汎用ソフトであるStanを用いて実装し、ベイズ統計の立場から分析しました。MCMCおよびベイズ統計についてはこちらの記事で(走り書きで)書いています。
上で見た記事ではいずれも対象が各クラスに属する確率のオッズ比に着目し、オッズ比の線形性のみを考慮したモデルです。このように統計モデルでは変数の背後に何かしらの分布を想定したり、変数間に線形的な関係を想定したりすることでモデルを構築します。
一方で、特定の分布や関係を仮定せず、与えられたデータに柔軟に対応することのできるモデルも存在します。そのようなモデルの例としてこちらの記事ではガウス過程回帰について取り上げました。
またガウス過程を様々なデータやモデルに応用できるよう、前回の記事ではガウス過程潜在変数モデルやカテゴリカルな変数に対応できるカーネル、予測分布の計算方法について説明しました。
今回の記事はこれらの記事の内容をフル活用し、多項ロジスティック回帰にガウス過程を適用したモデルを実装します。
最終目標は、対象が各クラスに属する確率の予測値を、データに柔軟にフィットさせることです。
本記事の構成は以下の通りとします。
当初本記事と前回の記事はひとつの記事として公開していましたが、余りにも長すぎる記事だったので、二つに分けて公開しなおしました。
データの入手
以前の記事でRのnnetパッケージを使って多項ロジスティック回帰分析をしたときに用いたものと同じデータを用いますある学校の生徒の属性と各生徒が選択した授業に関するデータです。
library(foreign)
ml <- read.dta("https://stats.idre.ucla.edu/stat/data/hsbdemo.dta")
head(ml)
## id female ses schtyp prog read write math science socst honors
## 1 45 female low public vocation 34 35 41 29 26 not enrolled
## 2 108 male middle public general 34 33 41 36 36 not enrolled
## 3 15 male high public vocation 39 39 44 26 42 not enrolled
## 4 67 male low public vocation 37 37 42 33 32 not enrolled
## 5 153 male middle public vocation 39 31 40 39 51 not enrolled
## 6 51 female high public general 42 36 42 31 39 not enrolled
## awards cid
## 1 0 1
## 2 0 1
## 3 0 1
## 4 0 1
## 5 0 1
## 6 0 1
今回も、general, academic, vocation の3つの授業の中から生徒が選択した結果(prog)を出力(目的変数)、write(書く力を得点化したもの)と家庭の経済状況の指標ses(low, middle, highに分類)の2変数を入力(説明変数)とし、モデルを組み立てていきます。
多項ロジスティック・ガウス過程モデル
モデルの確認
出力を$(N×1)$ベクトル$\mathrm{y}=(y_1,\ldots,y_N)^T$、入力を$(N×(I+J))$行列$\mathrm{W}=(\mathrm{w}_1,\ldots, \mathrm{w}_N)^T$とします。
$$ \mathrm{w}_n = (\mathrm{x}_n^T,\mathrm{z}_n^T) \tag{1} $$
$\mathrm{x}_n$、$\mathrm{z}_n$はそれぞれ要素数$I$の質的変数、要素数$J$の質的変数です。
$$ \left(x_{n1},\ldots,x_{nI}\right)^T=\mathrm{x}_{n} $$
$$ \left(z_{n1},\ldots,w_{nJ}\right)^T=\mathrm{w}_{n} $$
$\mathrm{y}$が$K$個の値をとるとき、$\mathrm{y}$が各値をとる確率を表す$(N×K)$行列$\mathrm{\Theta}=(\mathrm{\theta}_1, \ldots, \mathrm{\theta}_K)$を導入します。
ここで$(\theta_{k1},\ldots,\theta_{kN})^T=\mathrm{\theta}_k~~~(k=1,\ldots,K)$です。
$$ \mathrm{y} \sim \rm{Categorical}(\Theta)\tag{2} $$
$\Theta$は1行の要素の和をとると1になるので、各要素が$(-\infty,\infty)$の値をとる$(N×K)$行列$\mathrm{P}=(\mathrm{p}_1,\ldots,\mathrm{p}_K)$を導入し、下記のようにします。
ここで、$(p_{k1},\ldots,p_{kN})^T=\mathrm{p}_k~~(k=1,\ldots,K)$です。
$$ (\theta_{1n},\ldots,\theta_{Kn})^T = \rm{softmax}(\mathrm{P}_n^T)~~~(n=1,\ldots,N) \tag{3} $$
ここで$(p_{1n},p_{2n},\ldots,p_{Kn})=\mathrm{P}_n$です。
ガウス過程で推定する対象は、上記モデルの$\mathrm{P}$になります。多項ロジスティック回帰では、出力が任意の特定の値をとる確率を固定する必要があったので、それを踏まえて下記のようにおきます。
$$
\mathrm{p}_k = \begin{cases}
0~~~\mathrm{if}~k=1\\
\mathrm{L}\eta_k~~~\mathrm{if}~k=2,\ldots,K
\end{cases}\tag{4}
$$
$$ \mathrm{LL^T} = \mathrm{K}\tag{5} $$
$$ \eta_k=(\eta_{k1},\ldots,\eta_{kN}) \sim \rm{Normal}(0,1) ~~(k=2,\ldots,K)\tag{6} $$
ここで、$\mathrm{K}$は$(N×N)$のカーネル行列で、$(m,n)$成分をカーネル関数$k(\mathrm{w}_m,\mathrm{w}_n)$とします。カーネル関数の設定を工夫することで、線形モデルから得られた知見やデータの特徴(カテゴリカル変数が含まれる点)などをモデルに反映させていきます。
カーネル関数の設定方法
本記事では2つのカーネル関数を設定し、2段階に分けて多項ロジスティック回帰・ガウス過程モデルを実行します。
モデル1 線形カーネル + isotropic correlationカーネル
量的変数writeの影響は線形カーネルで取り入れ、カテゴリカル変数sesの影響をPDUDEである$\mathrm{T}$で考慮する、という構造です。$\mathrm{T}$の各要素はisotropic correlation functionで出力されます。
このカーネル関数をロジスティック回帰・ガウス過程モデルに用いることで、これまでの記事(1)、(2)で得られた結果と同じ結果が得られることを確認し、モデルの妥当性チェックを行います。
カーネル関数は下になります。
$$ \theta_1\sum_{i=1}^{I}x_{mi}x_{ni} + \theta_2\sum_{j=1}^J\mathrm{T}(z_{nj},z_{mj}) = k(\mathrm{w}_m,\mathrm{w}_n) \tag{7} $$
ここで、
$$
\mathrm{T} = \left(
\begin{array}{ccc}
1 & c & \cdots & c \\
c & 1 & \cdots & c \\
\vdots & \vdots & \ddots & \vdots \\
c & c & \cdots & 1
\end{array}
\right)\tag{8}
$$
は、前回の記事の式$(22)$、$(23)$あたりで説明したものす。
ハイパーパラメータは$\theta_1$、$\theta_2$、$c$の3つです。
なお、$(7)$式第一項の線形カーネルの部分は、ガウス過程として扱わないで前回の記事の式$(1’)$の$\beta\mathrm{f}(\mathrm{w})$で扱うこともできるのですが、今回はフルガウス過程で実行してみます。
モデル2 線形カーネル + (ガウスカーネル × isotropic correlationカーネル)
量的変数writeの影響をモデル1のように線形的に把握するだけでなく、線形モデルでは誤差として扱われてしまう要素まで結果に取り入れるため、線形カーネルとガウスカーネルを組み合わせて量的変数の影響を予測します。質的変数の影響はモデル1と同様にisotropic correlationカーネルで予測します。
カーネル関数は下になります。
$$ \theta_1\sum_{i=1}^{I}x_{mi}x_{ni} +\theta_2\rm{exp}\left(-\cfrac{1}{2\rho^2}\sum_{i=1}^{I}(x_{im}-x_{in})^2-\sum_{j=1}^{J}\rm{ln}\left(\cfrac{1}{c}\right)I[r\neq{s}]\right) \tag{9} $$
ハイパーパラメータは$\theta_1$,$\theta2$,$\rho$,$c$の4つです。
モデル1の実装と結果の確認
モデル1を実行するStanコードを以下のようになります。
//model2
data{
int<lower=2> K; //カテゴリ数
int<lower=1> N1; //データ数
int N2; //予測入力数
int<lower=1> I; //量的変数の数
int<lower=1> J; //質的変数の数
int M[J]; //各質的変数のカテゴリ数
int<lower=1, upper=K> y[N1]; //出力ラベル
int<lower=1, upper=max(M)> x1_j[N1,J]; //入力(質的変数)
vector[I] x1_i[N1];//入力(量的変数)
int<lower=1, upper=max(M)> x2_j[N2,J]; //予測したい点(質的変数)
vector[I] x2_i[N2]; //予測したい点(量的変数)
}
transformed data{
real delta = 1e-9;
int<lower=1> N = N1 + N2;
int<lower=1, upper=max(M)> x_j[N,J]; //入力(質的変数)と予測入力(質的変数)を縦に繋げたもの
vector[I] x_i[N]; //入力(量的変数)と予測入力(量的変数)を縦に繋げたもの
//以下でx1_iとx2_i,x1_jとx2_jを縦に結合し、新たな行列x_i,x_jをそれぞれ作成する
for(n in 1:N1){
for(j in 1:J){
x_j[n,j] = x1_j[n,j];
}
}
for(n in 1:N2){
for(j in 1:J){
x_j[(N1+n),j] = x2_j[n,j];
}
}
for(n in 1:N1) x_i[n] = x1_i[n];
for(n in 1:N2) x_i[N1+n] = x2_i[n];
}
parameters{
vector[N] eta[(K-1)]; //潜在変数
vector<lower=0>[2] theta;
vector<lower=0, upper=1>[J] C;
}
transformed parameters{
vector[N] f[(K-1)];
row_vector[K] p[N]; //ソフトマックス関数に投げる値
//この中でカーネル関数を定義、ガウス過程の関数fを作成
{
matrix[N,N] L_K[(K-1)];
matrix[N,N]linear_kernel;
matrix[N,N]isotropic_correlation_kernel = rep_matrix(0,N,N);//初期値を0に設定。
matrix[N,N] kernel_matrix[(K-1)];
matrix[max(M),max(M)] PDUDE[J];
//compound symmetric correlation matrix を作成
for(j in 1:J){
for(n in 1:(max(M)-1)){
PDUDE[j][n,n] = 1;
for(m in (n+1):max(M)){
PDUDE[j][n,m] = C[j];
PDUDE[j][m,n] = PDUDE[j][n,m];
}
}
PDUDE[j][max(M),max(M)] = 1;
}
//isotropic_correlation_kernelを生成
for(j in 1:J){
for(n in 1:N){
for(m in 1:N){
isotropic_correlation_kernel[n,m] += PDUDE[j][x_j[n,j],x_j[m,j]];
}
}
}
//linear_kernel_matrixを生成。切片項はisotropic_correlation_kernelで捉えることにした
for(n in 1:N){
for(m in1:N){
linear_kernel[n,m] = dot_product(x_i[n],x_i[m]);
}
}
//kernel_matrixを作成
for(k in 1:(K-1)){
kernel_matrix[k] = theta[1] * linear_kernel + theta[2] * isotropic_correlation_kernel;
for(n in 1:N){
kernel_matrix[k][n,n] += delta;
}
}
for(k in 1:(K-1)){
L_K[k] = cholesky_decompose(kernel_matrix[k]);
f[k] = L_K[k] * eta[k];
}
}
// pの作成 1列目は0に固定 2列目以降に独立のガウス過程を指定
for(n in 1:N){
p[n,1] = 0;
for(k in 1:(K-1)){
p[n,(k+1)] = f[k,n];
}
}
}
model{
//事前分布
theta ~ student_t(4,0,2);
C ~ normal(0,0.1);
//モデル部分
for(k in 1:(K-1)){
for(n in 1:N){
eta[k,n] ~ std_normal();
}
}
for(n in 1:N1){
y[n] ~ categorical_logit(p[n]');
}
}
generated quantities{
vector[K] pred[N2];
for(n in 1:N2){
pred[n] = softmax(p[(N1+n)]');
}
}
入力データを命令するdata{}ブロックでは、入力データ(x1_i、x1_j)を量的変数・質的変数で分けて指定しています。また、予測したい入力点(x2_i、x2_j)も指定しています。
transformes data{}ブロックでは、式$(12)$の計算を実行するため、入力(実現値)と予測したい入力点のデータを量的変数・質的変数毎に縦に繋げています。
transformed parameter{}ブロックでは、まず、式$(8)$の行列をPDUDEという呼称で作成しています。次に、issotropic_correlation_kernelとして、PDUDEを参照しながらcompound symmetric correlation matrixを作成しています。
また、linear_kernelとして線形カーネルの要素を作成しています。線形カーネルはStanに実行されたdot_product()が便利です。
さらに、kernel_matrixとして式$(7)$のカーネル関数を各要素に持つカーネル関数を作成します。
このように、線形カーネル・isotropic_correlation_kernelカーネルを作成し、それらを結合させてカーネル行列を作成し、最後に既述の方法でガウス過程に従う$\mathrm{f}$の定義までをtransformed parameter{}で命令しています。
model{}ブロックでは、まず事前分布を式$(7)$の$\theta_1$、$\theta_2$、式$(8)$の$c$で、適当に指定しています。
また、前回記事式$(9)$中段の設定をeta ~ std_normal()として指定し、多項ロジスティック回帰モデルの式$(2)$、式$(3)$をy[n] ~ categorical_logit(p[n]')としています。
generated quantities{}ブロックでは、modelブロックでは作成しなかった入力点x2_i、x2_jにおける予測値をpredとして指定しています。
このStanファイルを実行するコードは以下になります。
# progの3要素を数字に置き換えるための表を作成
progid <- c(1,2,3)
names(progid) <- c("academic","general","vocation")
# sesの3要素を数字に置き換えるための表を作成
sesid <- c(1,2,3)
names(sesid) <- c("low","middle","high")
library(makedummies)
library(tidyr)
library(dplyr)
d2 <- ml %>% mutate(sesid = sesid[paste(ses)]) %>%
mutate(progid = progid[paste(prog)]) %>% mutate(write=(write-mean(write))/sd(write)) %>% select(c(sesid, write, progid))
#x1:入力点
x1_j <- data.frame(d2[,-c(2,3)]) # 入力(質的変数)
x1_i <- data.frame(d2[,-c(1,3)]) # 入力(量的変数)
N1 <- nrow(x1_i)
#x2:予測入力点
x2_j <- data.frame(sesid = c(rep(1,41),rep(2,41),rep(3,41))) # 予測入力点(質的変数)
x2_i <- data.frame(write = (rep(c(30:70),3)-mean(ml$write))/sd(ml$write)) # 予測入力点(量的変数)
N2 <- nrow(x2_i)
#y:出力点
y <- d2[,3]
K <- 3
J <- 1 #質的変数の数
I <- 1 #量的変数の数
M <- c(3) #各量的変数のカテゴリ数
dim(M) <- 1
data <- list(x1_i=x1_i,x1_j=x1_j,x2_i = x2_i,x2_j=x2_j,N1=N1,N2=N2,K=K,y=y,J=J,I=I, M=M)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
fit_cate1 <- stan(file="model2.stan", data=data, pars = c("pred","theta","C"), warmup = 400, iter = 1500, chains=4, seed=1234)
計算にかかった時間はsurface laptop2 Corei5-8250Uで約3000秒でした。 ガウス過程は逆行列の計算などを含むので、工夫をしないとどうしても計算に時間がかかってしまうようです。
ハイパーパラメータの事後分布は以下のようになりました。
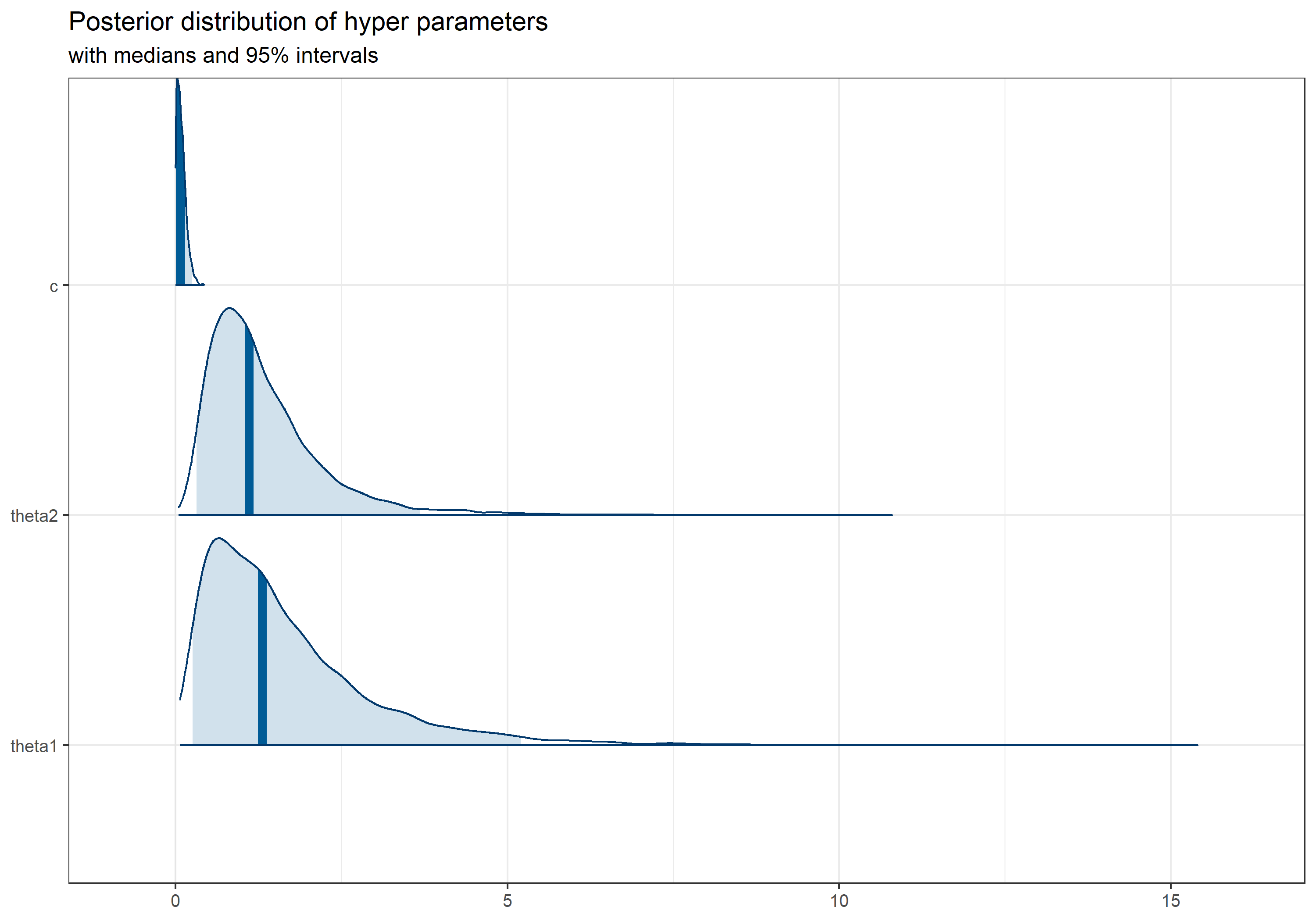
予測結果は以下のようになりました。描画の為のコードは以前の記事を参照してください。

rのパッケージnnetのmultinom()関数を使ったときや、Rstanで線形予測子Versionの多項ロジスティック回帰を実行したときの結果と同じ結果が得られていることが分かります。
以上、sotropic correlationカーネルを含んだモデル全体が正常に動くことを確認し、次の分析に進みます。
モデル2の実装と結果の確認
モデル2を実行するStanコードを以下のようになります。
//model3
data{
int<lower=2> K; //カテゴリ数
int<lower=1> N1; //入力データの数
int N2; //予測したい入力点の数
int<lower=1> I; //量的変数の数
int<lower=1> J; //質的変数の数
int M[J]; //各質的変数のカテゴリ数
int<lower=1, upper=K> y[N1]; //出力ラベル
int<lower=1, upper=max(M)> x1_j[N1,J]; //入力(質的変数)
vector[I] x1_i[N1];//入力(量的変数)
int<lower=1, upper=max(M)> x2_j[N2,J]; //予測した入力点(質的変数)
vector[I] x2_i[N2]; //予測したい入力点(量的変数)
}
transformed data{
real delta = 1e-9;
int<lower=1> N = N1 + N2;
int<lower=1, upper=max(M)> x_j[N,J]; //入力(質的変数)と予測入力(質的変数)を縦に繋げたもの
vector[I] x_i[N]; //入力(量的変数)と予測入力(量的変数)を縦に繋げたもの
matrix[max(M),max(M)] inv_I; //対角成分が0、それ以外が1の行列を生成
//以下でx1_iとx2_i,x1_jとx2_jを縦に結合し、新たな行列x_i,x_jをそれぞれ作成する
for(n in 1:N1){
for(j in 1:J){
x_j[n,j] = x1_j[n,j];
}
}
for(n in 1:N2){
for(j in 1:J){
x_j[(N1+n),j] = x2_j[n,j];
}
}
for(n in 1:N1) x_i[n] = x1_i[n];
for(n in 1:N2) x_i[N1+n] = x2_i[n];
//inv_Iの作成
for(n in 1:(max(M)-1)){
inv_I[n,n] = 0;
for(m in (n+1):max(M)){
inv_I[n,m] = 1;
inv_I[m,n] = 1;
}
}
inv_I[max(M),max(M)] = 0;
}
parameters{
vector[N] eta[(K-1)]; //潜在変数
vector<lower=1>[2] //theta;線形カーネルと「ガウスカーネル・isotropic correlationカーネル」の重みを決定するハイパーパラメータ
vector<lower=0, upper=1>[J] C; //isotropic correlationカーネルのハイパーパラメータ
real<lower=0, upper=0.9> rho; //ガウスカーネルのshapeパラメータ
}
transformed parameters{
vector[N] f[(K-1)];
row_vector[K] p[N]; //ソフトマックス関数に投げる値
//この中でカーネル関数を定義、ガウス過程に従う関数fを作成
{
matrix[N,N] L_K[(K-1)]; //カーネル行列をコレスキー分解した行列L。(出力がとる値)-1の数だけ準備する
matrix[N,N]linear_kernel; //線形カーネル
matrix[N,N]distance_L2_01_kernel; //。ガウスカーネル×isotropic correlation カーネル。logスケールでL2距離と0-1距離の成分を含んでいる
matrix[N,N] kernel_matrix[(K-1)]; //最終的に作成するカーネル関数
//linear_kernelを生成
for(n in 1:N){
for(m in1:N){
linear_kernel[n,m] = dot_product(x_i[n],x_i[m]);
}
}
//distanceL2_01_kernelを生成
{
matrix[N,N] distance_L2; //L2距離
matrix[N,N] distance_01 = rep_matrix(0,N,N); //inv_Iに依存した0-1距離
for(n in 1:N){
for(m in 1:N){
distance_L2[n,m] = dot_self((x_i[n]-x_i[m]) ./ rho);
}
}
for(j in 1:J){
for(n in 1:N){
for(m in 1:N){
distance_01[n,m] += log(1/C[j])*inv_I[x_j[n,j],x_j[m,j]];
}
}
}
for(n in 1:N){
for(m in 1:N){
distance_L2_01_kernel[n,m] = exp(-0.5 * distance_L2[n,m] -distance_01[n,m]);
}
}
}
//kernel_matrixを作成
for(k in 1:(K-1)){
kernel_matrix[k] = theta[1] * linear_kernel + theta[2] * distance_L2_01_kernel;
for(n in 1:N){
kernel_matrix[k][n,n] += delta;
}
}
for(k in 1:(K-1)){
L_K[k] = cholesky_decompose(kernel_matrix[k]);
f[k] = L_K[k] * eta[k];
}
}
// pの作成 1列目は0に固定 2列目以降に独立のガウス過程を指定
for(n in 1:N){
p[n,1] = 0;
for(k in 1:(K-1)){
p[n,(k+1)] = f[k,n];
}
}
}
model{
//事前分布
theta ~ student_t(4,1,2);
rho ~ inv_gamma(0.1, 0.1);
C ~ normal(0, 0.1);
//モデル部分
for(k in 1:(K-1)){
for(n in 1:N){
eta[k,n] ~ std_normal();
}
}
for(n in 1:N1){
y[n] ~ categorical_logit(p[n]');
}
}
generated quantities{
vector[K] pred[N2];
for(n in 1:N2){
pred[n] = softmax(p[(N1+n)]');
}
}
モデル1との違いは、transformed parameters{}ブロックにおけるカーネル行列作成の部分と、model{}ブロックにおける事前分布設定の部分になります。
transformed parameters{}ブロックでは、linear_kernelとして式$(9)$第1項の部分(線形カーネル)の$\theta_1$を除いた部分を、distance_L2_01_kernelとして式$(9)$第2項の$\theta_2$を除いた部分を作成しています。またdistance_L2_01_kernelは、distance_L2として$\sum_{i=1}^{I}(x_{im}-x_{in})^2$を、distance_01_kernelとして$\sum_{j=1}^{J}ln\left(\cfrac{1}{c}\right)I[r\neq{s}]$をそれぞれ作成し、それらを式$(9)$に従って合成することで作成しています。
ハイパーパラメータの事前分布の設定はかなり苦戦しました。最終的に以下の事前分布を採用しています。
$$ \theta_1 \sim \rm{Student\verb|_|t}(4,1,2) ~~~\theta_1 \geq 1 $$ $$ \theta_2 \sim \rm{Student\verb|_|t}(4,1,2) ~~~\theta_2 \geq 1 $$ $$ \rho \sim \rm{invGamma}(0.1,0.1)~~~0 \leq \rho \leq 0.9 $$ $$ c \sim \rm{Normal}(0,0.1) $$
$\theta_1$、$\theta_2$については弱情報事前分布として、自由度4、期待値1、スケールパラメータ1の半t分布を採用しています。
$\rho$については、Stanマニュアルを参照して、0付近の値を避けることができつつも小さな値にとがった山を持ち、かつ十分大きな値にも対応可能な逆ガンマ分布を採用しています。
$c$については、0付近の値をとることが想定されるため、期待値0、標準偏差0.1の切断正規分布を採用しています。
様々な事前分布を試していたのですが、ガウスカーネルにおいて、shapeパラメータ$\rho$とrateパラメータ$\theta$の比が重要なようで、shapeパラメータに比べてrateパラメータが十分大きいと、出力値の変化の傾きが小さくなり、前回記事の式$(1)$の誤差項を捉えてくれなくなってしまいます。この点についてはStanマニュアルにも以下の記載があります。
Perhaps most importantly, the parameter $\rho$ and $\alpha$ are weakly identified Zhang(2004). The ratio of the rwo parameters is well-identified…
今回の場合、$\rho$に値の上限を設定しないとどうしても$\rho$が大きくなってしまい、予測結果もモデル式1と変わらなくなってしまいました。しかしそれはこのモデルの意図した結果ではありません。
以前の[ガウス過程のシミュレーション結果](https://rmorita-stat.github.io/2020/06/gaussianprocess/# ガウス過程のシミュレーション)を見ると、標準化されたデータの場合、shapeパラメータ、rateパラメータともに1前後でちょうどよいガウス過程からの出力が得られそうであることが確認できます。よって、今回はrateパラメータに0.9の上限を設け、shapeパラメータも下限値1を設定することで、少し変化の傾きが急な出力を得られるように強要することにします。
上記のStanファイルを実行するコードは以下になります。
data <- list(x1_i=x1_i,x1_j=x1_j,x2_i = x2_i,x2_j=x2_j,N1=N1,N2=N2,K=K,y=y,J=J,I=I, M=M)
rstan_options(auto_write = TRUE)
options(mc.cores = parallel::detectCores())
fit_cate2 <- stan(file="model3.stan", data=data, pars = c("pred","rho","theta","C"), warmup = 400, iter = 1500, chains=4, seed=1234)
計算にかかったた時間は確かおよそ9800秒でした。2時間以上かかっていますね。PCもうなり声をあげていたので冷却対策など必要かもしれません。
ハイパーパラメータの事後分布は以下のようになります。
posterior_fit0_2 <- rstan::extract(fit_cate2)
library(bayesplot)
plot_title <- ggtitle("Posterior distribution of hyper parameters", "with medians and 95% intervals")
p1 <- mcmc_areas(as.matrix(fit_cate2),
regex_pars = c("theta"),prob=0.95, area_method = "equal height") +
scale_y_discrete(labels=c("theta1","theta2")) + theme_bw(base_size=12)
p2 <- mcmc_areas(as.matrix(fit_cate2),
regex_pars = c("C","rho"),prob=0.95, area_method = "equal height") +
scale_y_discrete(labels=c("c","rho")) +
theme_bw(base_size=12)
library(gridExtra)
g1 <- ggplot_gtable(ggplot_build(p1))
g2 <- ggplot_gtable(ggplot_build(p2))
Width <- unit.pmax(g1$widths, g2$widths)
Height <- unit.pmin(g1$heights, g2$heights)
g1$widths <- Width
g2$widths <- Width
g1$heights <- Height
g2$heights <- Height
p <- gridExtra::grid.arrange(g1,g2,ncol=1, top="Posterior distribution of hyper parameters (with medians and 95% intervals)")
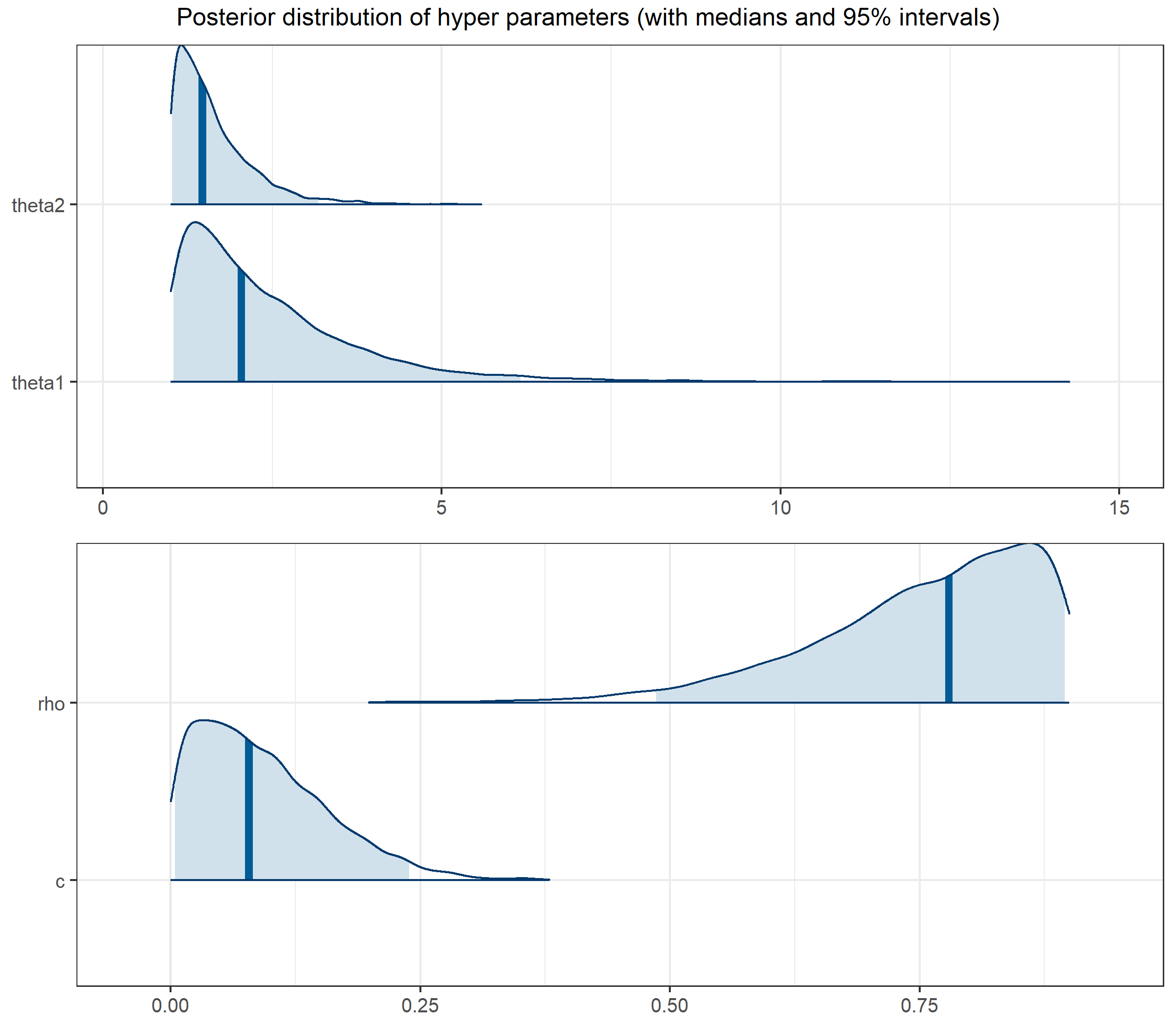
$\rho$が頑張って大きな値をとろうとしている様子が見えますが、そこは抑えてもらっています。何だかかわいそう…
最後に、予測結果を描画します。
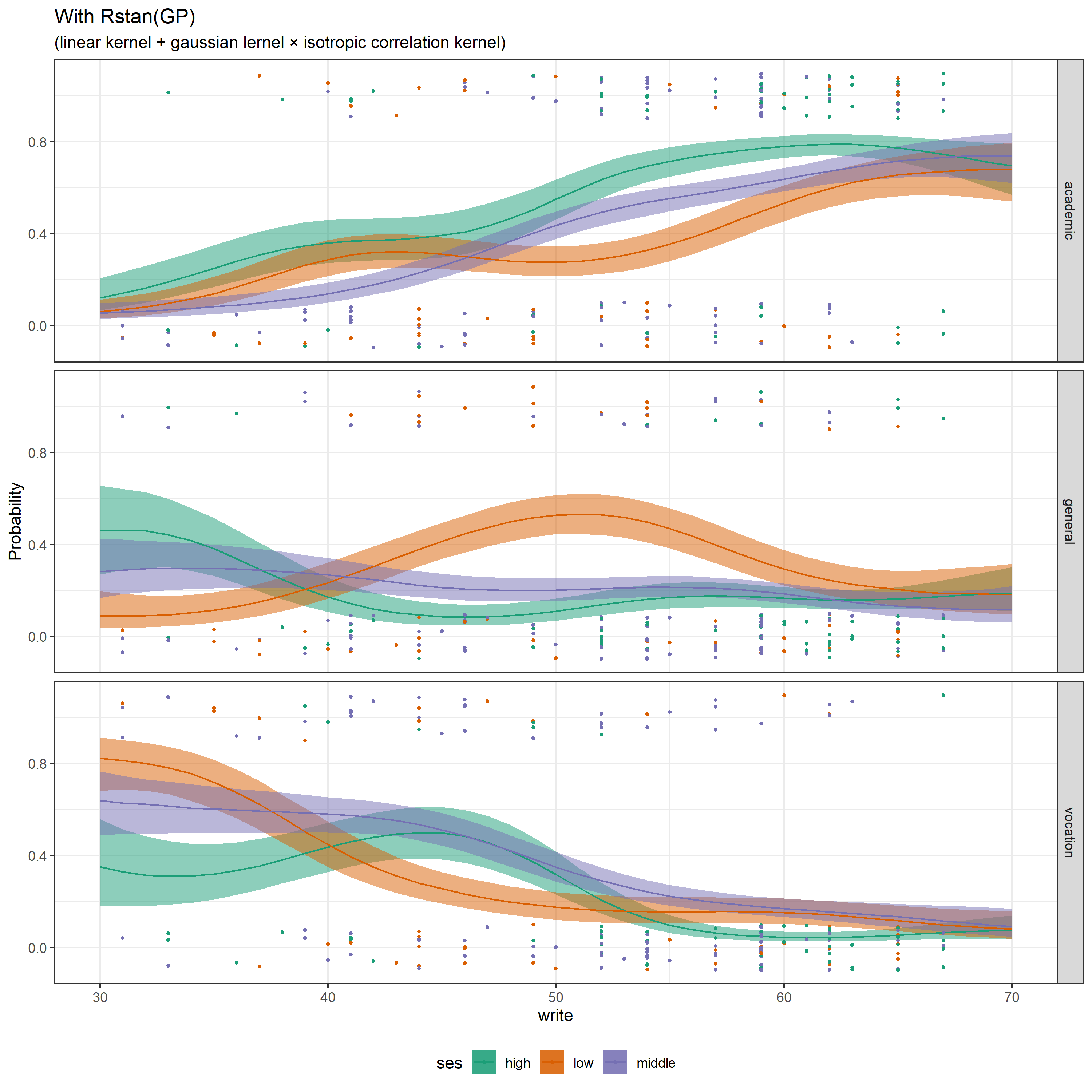
線形モデルでは読み取ることが出来なかった傾向がうまく捉えられています。例えば、読み書きの能力が50前後のses=lowの生徒はgeneralの授業をとる傾向にあること、読み書きの能力が45前後のses=highの生徒はacademicの授業をとる確率とvocationの授業をとる確率が同程度である様子などが確認できます。
It’s so brilliant>🐢
このように、線形モデルでは誤差として結果に反映されなかった事象もうまくとらえることが出来るのがガウス過程の魅力です。パラメータの事後分布や推測値よりデータの生成過程を考察する、という目的には不向きかもしれませんが、予測の観点から見れば非常に便利ではないでしょうか?。
まとめ
今回はガウス過程を多項ロジスティック回帰に取り込んだモデルの実装を行いました。その過程で、ガウス過程潜在変数モデルやカテゴリカルデータを取り入れたガウス過程等、前回の記事で説明したガウス過程の応用手法を用い、それらが正常に機能することを確かめました。
また、ガウス過程のように特定の分布を想定しないで、データに応じてモデルの複雑さを決定するパラメータを調整するベイズモデルはノンパラメトリックベイズモデルと呼ばれています。
この記事で、以前に述べたガウス過程の活用方法の1つ目(下記)を紹介した形です。
- 一般化線形モデルの線形予測子をガウス過程に置き換え、柔軟なモデルに豹変させる
多項ロジスティック回帰の記事も3つ目になりましたが、これで最後になります。最近はアウトプットに力を注いでいて投稿頻度も多かったですが、今後暫くはインプットに集中したいと考えており、投稿しない月が続くかもしれません。
Enjoy Stan!
