はじめに
秋は晴天の日が多いですネ。晴れた空の日曜日は外に出かけてみたくもなりますが、草野さんは部屋で昨日の夢を思い出しながら妄想するのもいいと言っています。なるほど…
さてこの記事はStan Advent calendar12月12日にエントリーしている記事(未投稿)を補完するために先に作成した記事になります。
この記事では多変量解析の一つである対応分析を取り上げます。
対応分析は多変量のカテゴリカルデータに用いられる分析で、分割表の結果を視覚的に表現するために使われる統計的手法です。
実は対応分析は私の修士研究で使用した解析手法なのですが、対応分析の付置はデータ数に依存しないことから、座標を得るだけでその信頼性が確認できないところに当時問題を感じていました。
この問題に対しベイズ的なアプローチをとることで解決できないかと錯誤した結果、うまくいったぽいので、Stanアドベントカレンダーではその結果について記事にする予定です。
本記事ではその前段階として、対応分析の理論的な枠組みと結果の解釈の方法などについて理解した範囲でまとめます。
本記事の構成は以下のとおりとします。
参考にした論文はこちらです。
この論文はもうだいぶ古いものですが、対応分析の理論が簡潔に記載されています。また、先に述べた対応分析の付置の信頼性の問題を解決してくれています1が、今回は信頼区間の問題には極力触れずにいきます。
対応分析について
対応分析とは分割表2など、カテゴリカルな行と列のデータを視覚的に表現することで、項目間の関係を把握しようとする手法です。コレスポンデンス分析とも呼ばれ、数理的には林先生の数量化理論第Ⅲ類と同等のものとされています。
対応分析法がやろうとしていること
$i$行$j$列が$f_{ij}$($i=1 … M$、$j = 1 … N$)である$M$行$N$列の分割表について考えます。
以下、この分割表の行項目$I$を、関係性を把握したい対象、列項目$J$を変量とみなして説明します。
各行・列および全項目の総和を以下のように表記します。
$X$の($i,j$)成分$x_{ij}$は以下のようになっています。
行項目$I$の$i_1$番目と、$i_2$番目の個体の間の$\mathcal{\chi}^2$距離は、
対応分析が$(1)$式で計算される行列の主成分分析であるということは、つまり、対応分析とは$(2)$式で定義された$\mathcal{\chi}^2$距離に関する変量の関係を最大限に説明できる軸を求め、それらの軸上に各項目を配置することで、項目間の関係性を視覚的に表示しようとする分析手法である、ということになります3。
行項目・列項目の座標の求め方
ここからは基本的に$\boldsymbol{X}$に関する主成分分析についての話です。項目$J$についても同様の行列計算・固有値分解を実行することで軸・座標を得ることができます。ただ、項目$I$と項目$J$それぞれで同じ軸が得られるというところの理論がよくわかりません。ここではそのへんの話は「そういうもの」とさせてください…
$\mathbf{1}_m = (1,\ldots,1) ∈ R^m$として
…いや冗談だろう、$\boldsymbol{X}$の分散共分散行列は
とにかく、$(4)$式の$\boldsymbol{\Sigma}$について固有値問題を解いて、得られた固有値を最大固有値から順に$\lambda_{1},\lambda_{2}\ldots,\lambda_{N}$、これらに対応する固有ベクトルを順に$\boldsymbol{l}_1,\boldsymbol{l}_2,\boldsymbol,\boldsymbol{l}_N$とします。これらを用いて、第$k$主成分ベクトルによる項目$I$の数量化スコア$\boldsymbol{z}_{k} = (z_{1k}, \ldots, z_{Nk})$を計算します。
これは主成分分析のスコアの計算と同じですね。純粋に項目$I$について主成分ベクトルに対する写像を得ています。
項目$J$の数量化スコア$\boldsymbol{z}^{*}_k$は、項目$I$と同様にして計算することもできますが、項目$I$の数量化スコアから求めることもできるようです。証明は未確認ですが、この式を信用していくことにします。
$(5)$式および$(6)$式により得られた数量化スコアを同じ図の中に付置したものを同時付置図といい、同時付置図をもとに項目間の関係性をみることになります。
得られた軸の性質
対応分析によって得られた軸に関する性質をまとめておきます。これらの性質は付置図について考察する際の前提にもなります。またこれらの性質はすべて主成分分析からきたものです。ここで$K=\rm{min}(\mathcal{m},\mathcal{n}) -1$56とします。
分析例
Rを用いた計算例
実際に対応分析をやってみます。
サンプルデータは参考論文にあった貴乃花現役時代の大相撲6場所の幕内力士20人の勝ち数と決まり手の関係です。
smo_data <- matrix(data=c(15,15,0,0,1,0,1,19,9,7,12,1,3,3,4,22,0,11,2,0,4,
14,3,11,3,1,1,6,24,7,5,5,0,0,2,30,2,6,2,2,0,2,
11,13,5,6,2,1,4,25,8,10,7,5,3,1,13,31,3,3,0,2,3,
8,2,19,3,2,0,4,28,8,8,2,1,0,7,9,3,14,11,2,0,4,
5,3,12,11,4,0,7,7,1,18,0,1,0,11,12,6,1,12,7,2,2,
25,2,11,3,1,0,1,16,4,18,3,0,0,5,23,2,6,5,1,0,2,
7,17,2,16,3,0,1,2,8,1,11,1,0,2),byrow=TRUE, ncol=7)
colnames(smo_data) <- c("寄り","押し","投げ","引き","送り","突き","その他")
rownames(smo_data) <- c("小錦","琴錦","貴闘力","霧島","栃ノ和歌","水戸錦","若ノ花",
"貴ノ花","武蔵丸","大翔山","安芸ノ島","三杉里","旭道山","舞の海",
"寺尾","琴の若","貴ノ浪","琴富士","隆三杉","春日富士")
分析例は以下になります7。変量の数は7なので、得られる軸は6つですが、同時付置図は第1軸と第2軸をもとに作成します。
# 主成分分析の対象行列作成 ------------------------------------------------------------
# apply()とか使わないでごめんなさい
N <- sum(smo_data)
m <- nrow(smo_data)
n <- ncol(smo_data)
p_i <- rep(NA, length=m)
for(i in 1:m){
p_i[i] <- sum(smo_data[i,])/N
}
P_i <- diag(p_i)
p_j <- rep(NA, length=n)
for(j in 1:n){
p_j[j] <- sum(smo_data[,j])/N
}
P_j <- diag(p_j)
P_ij <- smo_data/N
matpow <- function(x, pow=2) {
y <- eigen(x)
y$vectors %*% diag( (y$values)^pow ) %*% t(y$vectors)
}
X <- solve(P_i) %*% P_ij %*% matpow(P_j, pow=(-1/2))
# 論文の方法に則った対応分析 -----------------------------------------------------------
X_bar <- matrix(rep(colSums(X)/nrow(X),20), byrow=T, nrow=nrow(X))
X_cov <- t((X - X_bar)) %*% P_i %*% (X - X_bar)
X_pca <- eigen(X_cov)
## eigen() decomposition
## $values
## [1] 2.507433e-01 1.341368e-01 8.920454e-02 3.256496e-02 2.038708e-02 1.430728e-02
## [7] 6.775222e-17
## $vectors
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.22994960 0.71371157 -0.2438985 0.15461675 0.08409387 -0.06865717
## [2,] -0.68444371 0.08147953 0.5365504 -0.03442796 -0.09073808 0.19007387
## [3,] 0.57769184 -0.34733619 0.2671700 -0.07516444 -0.47057317 0.25705425
## [4,] -0.30345943 -0.48187904 -0.5352658 0.36673289 -0.18451979 -0.27445628
## [5,] -0.05982687 -0.19188089 -0.3935578 -0.38378721 0.44535231 0.64529649
## [6,] -0.09307838 0.04510096 -0.1558085 -0.82883709 -0.24428825 -0.45225825
## [7,] 0.20149856 -0.30376746 0.3399617 -0.02240822 0.68643479 -0.44363261
## [,7]
## [1,] -0.5852867
## [2,] -0.4375669
## [3,] -0.4255399
## [4,] -0.3812200
## [5,] -0.2065814
## [6,] -0.1176471
## [7,] -0.2881753
rikishi_coord1 <- X %*% X_pca$vectors[,1]
rikishi_coord2 <- X %*% X_pca$vectors[,2]
waza_coord1 <- 1/sqrt(X_pca$values[1]) * solve(P_j) %*% t(P_ij) %*% rikishi_coord1
waza_coord2 <- 1/sqrt(X_pca$values[2]) * solve(P_j) %*% t(P_ij) %*% rikishi_coord2
# 寄与率の表示 ------------------------------------------------------------------
varsum <- sum(X_pca$values[1:6])
cat(paste(sprintf("\nContribution Rate of dim%.f: %.3f", 1:6,X_pca$values[1:6]/varsum)))
## Contribution Rate of dim1: 0.463
## Contribution Rate of dim2: 0.248
## Contribution Rate of dim3: 0.165
## Contribution Rate of dim4: 0.060
## Contribution Rate of dim5: 0.038
## Contribution Rate of dim6: 0.026
# プロット --------------------------------------------------------------------
library(ggplot2)
library(ggrepel)
p <- ggplot() + theme_light(base_size=11) +
geom_point(data=data.frame(x=rikishi_coord1, y=rikishi_coord2), aes(x=x,y=y), shape=1, col="red") +
geom_point(data=data.frame(x=waza_coord1, y=waza_coord2), aes(x=x,y=y), shape=2, col="blue") +
geom_text_repel(data=data.frame(x=rikishi_coord1, y=rikishi_coord2, label=rownames(smo_data)),
aes(x=x,y=y,label=label)) +
geom_text_repel(data=data.frame(x=waza_coord1, y=waza_coord2, label=colnames(smo_data)),
aes(x=x,y=y,label=label)) +
labs(title="Correspondence Analysis", x="dim1", y="dim2")
p
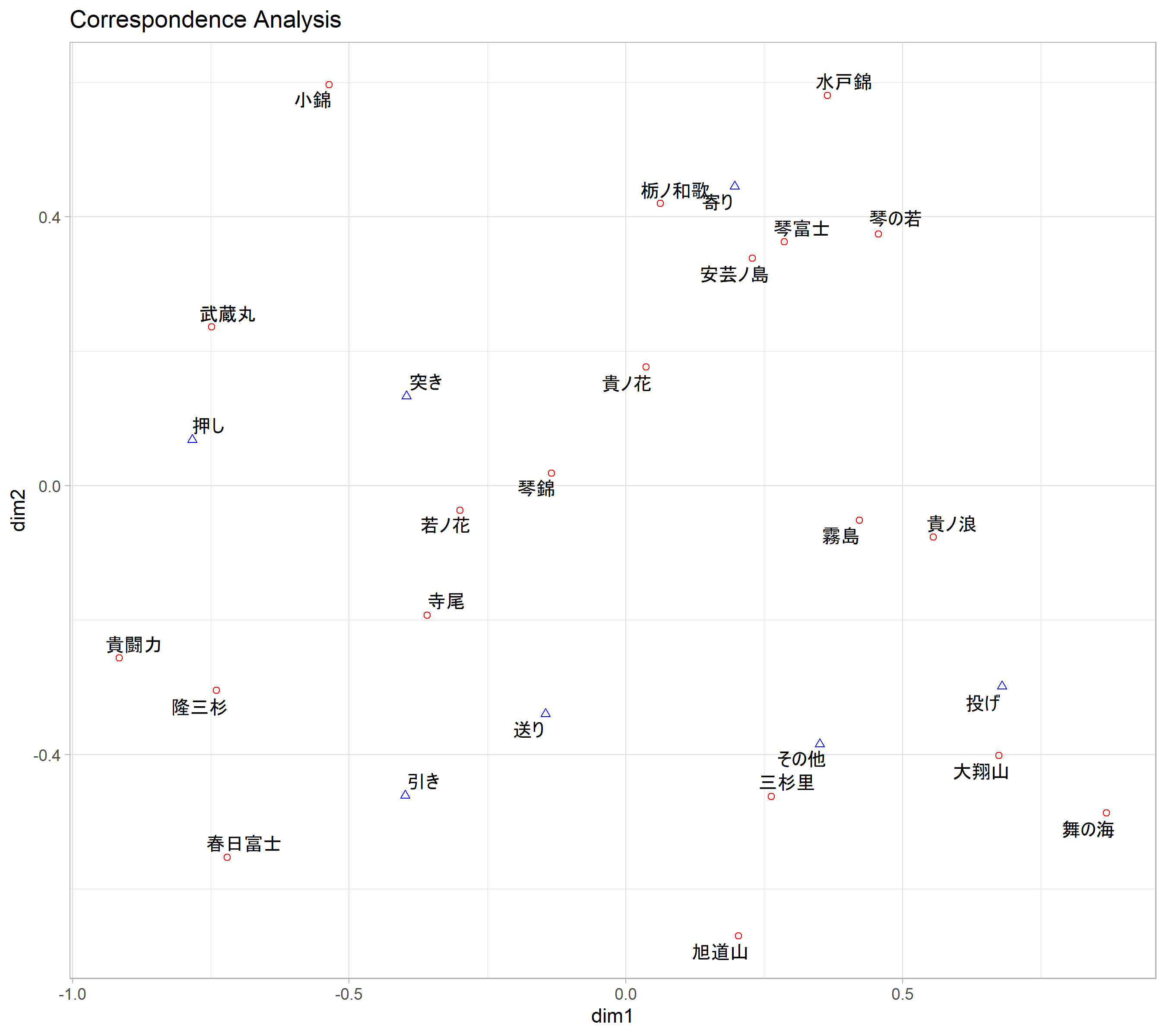
結果の解釈
以上の結果の解釈をしてみます。
まず、軸の寄与率を確認すると、第1軸で0.463、第2軸で0.248です。累積寄与率は0.711ですから、作成した同時付置図でデータの全分散の71%を説明できることになります。第3軸以降を用いて付置図を作成することも寄与率によっては勧められますが、ここでは71%の寄与率で十分とします。
では図の解釈に移ります。
同時付置図は各ポイントの相対的な位置関係と各軸に対する配置を基に考察されます。
まずはポイントの相対的な位置関係から。
ポイント間の距離は、主成分ベクトルによる写像を受けながらも、$\mathbf{χ}^2$距離に由来したものであることから、ポイント間の類似性を示します。ここで注意しなければならないことは、行項目、列項目は同じ軸上に付置されるものの、行項目同士・列項目同士の距離は定義されるが、行項目と列項目間の距離は定義されていない、ということです。
なので、例えば図の左下のほうに付置した貴闘力、隆三杉、春日富士は似たような決まり手を持つ力士である、というように解釈していくことになります。
次に各軸に対する配置を見てみます。
ここでは各ポイントの配置から、軸に解釈を与えたりします。参考の論文では以下のような解釈をしています。
第1主成分ベクトルでは「押し」、「引き」の係数が正の値で、「投げ」の係数が負の値で絶対値が大きく、第1軸は「突き押し型」^「投げを得意とする型」を表していると考えられる。第2主成分ベクトルでは「引き」、「投げ」、「その他」が正の値で、「寄り」が負の値で絶対値が大きく、第2軸は「組んで取る相撲」-「離れて取る相撲」を表していると考えられる。
実際に数名の力士の得意技を確認して確かめてみました。
春日富士は、突き、押しが得意な力士だそうで、同時付置図では左下に位置しています。第1軸に関して見れば確かに「突き押し型」の方向に位置することから、春日富士の得意な決まりてが反映された結果になっているようです。
舞の海秀平は関取時代は「平成の牛若丸」、「技のデパート」などと呼ばれたようで、豊富な技を使う力士だったようです。対照的な力士としては安芸乃島勝巳が挙げられ、「寄り」が得意な力士であったようです。第2軸に関して見れば、確かに春日富士は「離れて取る相撲」の方に位置しており、逆に「安芸乃島」は「組んで取る相撲」の方にいます。
このように、対応分析では分割表の数字の羅列から特に意味のある軸を作成し、視覚的に項目間の関係性を把握することができるようになります。
終わりに
対応分析の実践において有用であるにもかかわらず今回説明しなかったことや、次回触れたいことについてまとめておきます。
今回説明できなかったこと
こちらの文献に、ここで挙げる今回説明できなかったことが説明されています。修士のときも分からん!といいながらもお世話になっていました。
-
座標軸へのポイントの寄与
これは、座標軸のベクトルを決定するのに寄与しているポイントを意味するもので、各軸にとって重要なポイントを量的に示したものになります。
同時付置図の視覚的判断によらない軸の解釈方法とでもいうべきか? -
ポイントへの軸の寄与
これは、ポイントが、各座標軸によってどの程度表現されているかを示した数値になります。各ポイントの性質を同時付置図の視覚的判断に依らずに確認できる方法になるのかな? -
サプリメンタリーポイント
これは、一旦分割表の全行・列を用いて対応分析を実行したとき、同時付置図上で特定のポイントのみが他のポイントから極端に離れて付置される場合にとる手段です。 そのポイントを主成分分析の対象から一旦外し、得られたベクトルもとにそのポイントの写像を得る、という対処をします。
次回触れたいこと
次回は、座標の不確実性について考えたいと思っています。気付いたかもしれませんが、対応分析の同時付置図における座標は標本数に依存しないので、付置はできるがその信頼区間が分からない、という状態になっています。ベイズモデリングはこの問題への解決策の一つなのかなと考えています。
-
多項分布の正規近似に基づいて、解析的に信頼区間を求めているようで、私が試した方法とは別のアプローチをとっています。 ↩︎
-
「クロス集計表」とも呼ばれます。 ↩︎
-
文献によれば$(3)$式ではなく、$\sqrt{p_{j.}}$こそが$\boldsymbol{X}$の各列の平均値であると仰っているのですが、こちらについては簡単な計算で誤っていると確認したので、参考論文の$(3)$式を正とすることにします。 ↩︎
-
次元数が多く得られた項目の方については余剰の次元数を寄与率から度外視するのか…? ↩︎
-
行項目、列項目に対する主成分分析の結果のうち、得られた次元数が少ない方を次元の数とする、ということなのだが、$\mathrm{min}(m,n)$とはならないのは何故? ↩︎
-
RのFactoMineR::CAパッケージなどを使った整合確認は今後の自分に課す課題にします。参考論文における結果と異なるのであやしい気がする…←確認しました。今回の結果とFactoMineR::CAの結果はほぼ一致します。座標に関して言えば小数点第3位程度まで一致しました ↩︎
